Kezdőlap


Feladat:	B.4613	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Szakács Lili Kata
Füzet:	2015/március, 141 - 142. oldal		PDF \| MathML
Témakör(ök):	Feladat, Négyszögek geometriája, Terület, felszín, Vektorok
Hivatkozás(ok):	Feladatok: 2014/március: B.4613

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.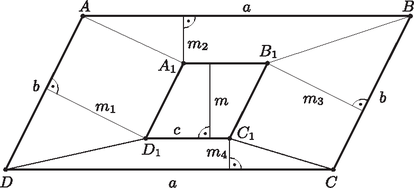

Megoldás. A feladat feltételei alapján az

A_{1} B_{1} C_{1} D_{1}

rombusz oldalai párhuzamosak az

A B C D

paralelogramma oldalaival. Használjuk az 1. ábra jelöléseit és legyen

T_{A D D_{1} A_{1}} = T_{1}

T_{A B B_{1} A_{1}} = T_{2}

T_{B C C_{1} B_{1}} = T_{3}

T_{C D D_{1} C_{1}} = T_{4}

, valamint

m_{a}

és

m_{b}

a paralelogramma megfelelő magasságai,

T

pedig a területe.

1. ábra

Ekkor

T_{1} + T_{3} = T_{2} + T_{4}

pontosan akkor teljesül, ha

\begin{matrix} \frac{(c + b)}{2} m_{1} + \frac{(c + b)}{2} m_{3} = \frac{(c + a)}{2} m_{2} + \frac{(c + a)}{2} m_{4}, \end{matrix}

vagyis

\begin{matrix} \frac{(c + b)}{2} (m_{1} + m_{3}) & = \frac{(c + a)}{2} (m_{2} + m_{4}), azaz \\ (c + b) (m_{b} - m) & = (c + a) (m_{a} - m) . \end{matrix}

Ez ekvivalens a

c m_{b} + T - b m = c m_{a} + T - a m

egyenlőséggel. Ebből következik, hogy a szemközti területek összegének egyenlősége nem függ a rombusz helyzetétől.
Helyezzük a rombuszt a paralelogramma

D

csúcsához úgy, hogy

D = D_{1}

legyen (2. ábra).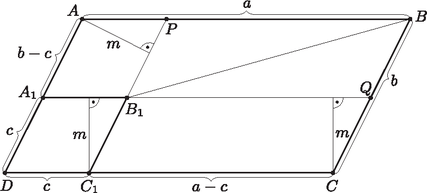

2. ábra

Ekkor az

A B B_{1} A_{1}

és

B C C_{1} B_{1}

trapézok területének egyenlőségét kell vizsgálni.
Húzzuk be a

B P B_{1} Q

paralelogramma

B B_{1}

átlóját. Ez felezi a paralelogramma területét, tehát elegendő az

A P B_{1} A_{1}

és

Q C C_{1} B_{1}

paralelogrammák területének egyenlőségét vizsgálni:

\begin{matrix} T_{A P B_{1} A_{1}} = (b - c) \cdot m és T_{Q C C_{1} B_{1}} = (a - c) \cdot m . \end{matrix}

Így a két terület pontosan akkor egyenlő, ha

(b - c) = (a - c)

, vagyis ha

a = b

. Tehát az

A B C D

paralelogramma pontosan akkor rombusz, ha

T_{1} + T_{3} = T_{2} {+ T}_{4}