Feladat:	B.4601	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Ágoston Péter ,  Csépai András ,  Di Giovanni Márk ,  Fekete Panna ,  Fonyó Viktória ,  Forrás Bence ,  Kúsz Ágnes ,  Maga Balázs ,  Simkó Irén ,  Williams Kada
Füzet:	2015/február, 82 - 85. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Tetraéderek, Terület, felszín, Esetvizsgálat
Hivatkozás(ok):	Feladatok: 2014/január: B.4601

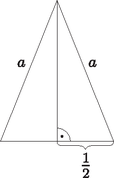
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. A tetraédernek négy csúcsa van, ezért bármely síkon lévő merőleges vetülete vagy háromszög, vagy konvex négyszög. Először azt az esetet vizsgáljuk, amikor a vetület háromszög. E háromszög csúcsai a tetraéder három csúcsának vetületei, a tetraéder negyedik csúcsának vetülete pedig a háromszögbe esik. Tehát a vetület területe megegyezik az egyik lap vetületének területével. Ismert, hogy ha egy $T$ területű sokszöget a síkjával $\alpha$ szöget bezáró síkra vetítünk és a vetület területe $T_v$, akkor $T_v=T\text{cos}\alpha$ (ennek bizonyítása megtalálható pl. Hajós György: Bevezetés a geometriába, 36.7. tétel). Tetraéderünknek kétfajta lapja van. Az egységnyi oldalú szabályos háromszög, ennek területe $\frac{\sqrt[]{3}}{4}$, valamint az olyan egyenlőszárú háromszög, amelynek alapja $1$, szárai pedig $a$ hosszúak. Az ilyen háromszög alaphoz tartozó magassága Pitagorasz tételéből következően $\sqrt[]{a^2-1/4}$ (1. ábra), ezért területe $\frac{\sqrt[]{a^2-1/4}}{2}$. Mivel $\text{cos}\alpha \le 1$, a tetraéder vetületének $t$ területére $\begin{array}{c}{\displaystyle t\le \frac{\sqrt[]{3}}{4}\mathrm{,}\text{illetve}t\le \frac{\sqrt[]{a^2-\frac{1}{4}}}{2}}\end{array}$ (1) teljesül.   1. ábra   A tetraéder szabályos háromszöglapjának síkjára vetítünk, akkor e lap vetülete önmaga, a negyedik csúcs vetülete pedig a tetraéder szimmetriája miatt e lap középpontjába esik (2. ábra), tehát ebben az esetben a vetület területe $t=\frac{\sqrt[]{3}}{4}$. Ha pedig a csúcsok betűzését úgy választjuk, hogy $AB=AC=AD=a$ és $BC=CD=DB=1$ teljesül és az $ABC$ lap síkjára vetítünk, akkor megmutatjuk, hogy a negyedik csúcs vetülete e lap belső pontja lesz, s így a vetület területe $t=\frac{\sqrt[]{a^2-1/4}}{2}$ (3. ábra). Mivel $A$ is és $D$ is egyenlő távolságra van $B$-től és $C$-től, ezért a $BC$ szakasz felezőmerőleges síkjában $A$ is és $D$ is benne van, tehát $AD\perp BC$. Ezért ha a $BC$ él felezőpontja $K$, akkor az $AKD$ sík merőleges az $ABC$ síkra. Vagyis $D$-nek az $ABC$ síkon lévő vetülete megegyezik az $AKD$ háromszög $D$-ből induló magasságának talppontjával. Ez pedig az $AK$ szakasz belső pontja, ugyanis a háromszög oldalainak hossza $AD=a$, $AK=\sqrt[]{a^2-1/4}$ és $KD=\frac{\sqrt[]{3}}{2}$, tehát leghosszabb ($AD$) oldalának négyzete kisebb, mint a másik két oldal négyzetének összege, vagyis $AKD$ hegyesszögű háromszög.   2. ábra 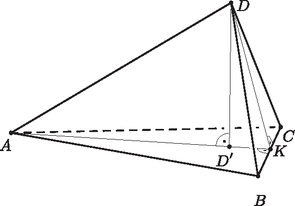    3. ábra   Ha a vetület konvex négyszög, akkor annak mind a négy csúcsa a tetraéder egy-egy csúcsának a vetülete, a négyszög $e$ és $f$ hosszú átlói pedig a tetraéder két kitérő élének vetületei. Sem a három darab 1 hosszú, sem a három darab $a$ hosszú tetraéderélek közt nincsenek kitérőek, ezért feltehetjük, hogy az $e$ hosszúságú átló valamely 1 hosszú, az $f$ hosszúságú átló pedig valamely $a$ hosszú tetraéderél vetülete. Merőleges vetítésnél bármely szakasz képének hossza legfeljebb akkora, mint az eredeti szakasz hossza, ezért $e\le 1$ és $f\le a$. Ismert, hogy ha egy konvex négyszög átlóinak hossza $e$ és $f$, az átlók szöge pedig $\phi$, akkor a négyszög területe $\left(ef\text{sin}\phi \right)/2$. Tehát ebben az esetben a tetraéder vetületének $t$ területére $\begin{array}{c}{\displaystyle t\le \frac{ef\text{sin}\phi }{2}\le \frac{ef}{2}\le \frac{a}{2}}\end{array}$ (2) teljesül. Válasszuk a csúcsok betűzését ugyanúgy, mint az előző példában, legyen továbbá az $AB$, $AC$, $DB$ és $DC$ élek felezőpontja rendre $E$, $H$, $F$ és $G$ (4. ábra). Ekkor az $ABD$ és $ACD$ háromszögekben $EF$ és $GH$ az $AD$ élhez, az $ABC$ és $BCD$ háromszögekben pedig $HE$ és $FG$ a $BC$ élhez tartozó középvonalak. Ezért $EF\parallel AD\parallel GH$ és $HE\parallel BC\parallel FG$. Vagyis az $E$, $F$, $G$ és $H$ pontok egy $\text{S}$ síkba esnek és paralelogrammát alkotnak. Továbbá a párhuzamosságok miatt az $AD$ és $BC$ egyenesek is párhuzamosak $\text{S}$-sel. Mivel merőleges vetítésnél a vetítés irányára merőleges szakaszok hossza nem változik, ez azt jelenti, hogy az $ABCD$ tetraéder $\text{S}$-en lévő merőleges vetülete egy olyan $A\text{'}B\text{'}C\text{'}D\text{'}$ négyszög, melyben $A\text{'}D\text{'}=AD=a$ és $B\text{'}C\text{'}=BC=1$. Továbbá $AD\perp BC$ miatt $A\text{'}D\text{'}\perp B\text{'}C\text{'}$ is fennáll. Vagyis az $ABCD$ tetraéder $\text{S}$ síkra eső merőleges vetületének $t$ területére 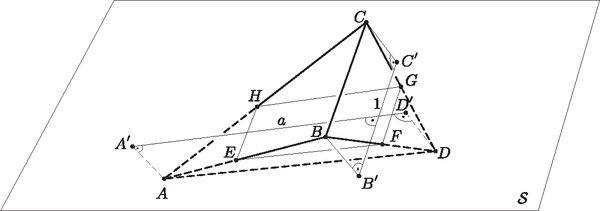$\begin{array}{c}{\displaystyle t=\frac{a\cdot 1\cdot \text{sin}{90}^{\circ }}{2}=\frac{a}{2}}\end{array}$ teljesül.   4. ábra   Most már csak azt kell megvizsgálnunk, hogy $a$ különböző értékei esetén az (1) és (2) egyenlőtlenségek közül melyik ad nagyobb felső korlátot a vetület területére. A feladatban leírt tetraéder nyilván pontosan akkor létezik, ha $a$ nagyobb, mint az egységnyi oldalú szabályos háromszög köré írható kör sugara, azaz ha $\frac{\sqrt[]{3}}{3}<a$. A $\frac{\sqrt[]{a^2-1/4}}{2}\le \frac{a}{2}$ egyenlőtlenség triviálisan teljesül, ezért azt kell meghatároznunk, hogy $\frac{\sqrt[]{3}}{4}\le \frac{a}{2}$ mikor áll fenn. Ez pontosan akkor teljesül, ha $\frac{\sqrt[]{3}}{2}\le a$. Tehát $\frac{\sqrt[]{3}}{3}<a\le \frac{\sqrt[]{3}}{2}$ esetén a tetraéder bármely síkon lévő merőleges vetületének területe legfeljebb $\frac{\sqrt[]{3}}{4}$, $\frac{\sqrt[]{3}}{2}\le a$ esetén pedig legfeljebb $\frac{a}{2}$ lehet.