Feladat:	B.4598	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Győrfi-Bátor András ,  Kabos Eszter
Füzet:	2015/február, 80 - 82. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Húrnégyszögek, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 2014/január: B.4598

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Legyen az $AE$ szakasz felezőpontja $F$, a $BE$ szakaszé pedig $G$. Az $ANE$ és $BLE$ háromszögek derékszögűek, ezért az $AE$, illetve $EB$ átmérőjű Thalész-körök ezen háromszögek köré írható körei, középpontjaik $F$ és $G$. Emiatt $AF=FE=FN$ és $BG=GE=GL$. Az $ABCD$ húrnégyszög, ezért $CBD\sphericalangle =CAD\measuredangle =\phi$, mivel a $CD$ ívhez tartozó kerületi szögek. Így az előbbi derékszögű háromszögekben a középponti és kerületi szögek összefüggését felhasználva $NFE\sphe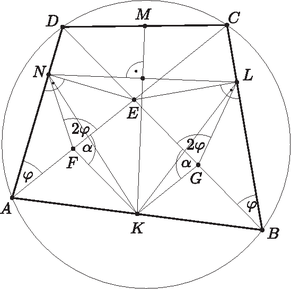ricalangle =2\phi$ és $EGL\sphericalangle =2\phi$ (1. ábra).   1. ábra   Az $ABE$ háromszögben $KF$ és $KG$ középvonalak, ezért az $EFKG$ négyszög paralelogramma, így szemközti szögei egyenlők: $EFK\sphericalangle =KGE\sphericalangle =\alpha$. Mivel $KG=FE=FN$ és $KF=GE=GL$, azért $NFK▵\cong KGL▵$, mivel két oldaluk és a közbezárt szög megegyezik. Tehát $NK=KL$, vagyis az $LNK$ háromszög egyenlő szárú, így $NL$ alapjának felezőmerőlegese átmegy a $K$ ponton. Hasonló gondolatmenettel belátható, hogy az $LNM$ háromszög is egyenlő szárú, és $LN$ alapjának felezőmerőlegese átmegy az $M$ ponton. Beláttuk, hogy az $LN$ szakasz felezőmerőlegese átmegy $K$ és $M$ pontokon is, vagyis $KM$ valóban merőleges az $NL$ szakaszra, sőt még felezi is. Az ábrán $CBD\sphericalangle$ és $CAD\sphericalangle$ hegyesszögek. Ilyenkor $L$ és $N$ pontok a $BC$ és $AD$ szakaszok belső pontjai. Ha a két szög tompaszög lenne, akkor ezek a pontok az $AD$ és $BC$ szakaszok meghosszabbításán keletkező külső pontok lesznek, de a gondolatmenet változatlanul működik. Ha a két szög derékszög, akkor a pontok a $CD$ szakasz Thalész-körén lesznek rajta, azaz $L$ és $N$ megegyezik az $A$ és $B$ pontokkal. Ekkor $KM$ egyenes a Thalész-kör átmérője, ami áthalad $LN$, azaz $AB$ húr felezőpontján, ezért éppen a húr felezőmerőlegese. 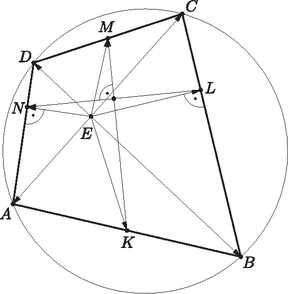  II. megoldás. Dolgozzunk vektorokkal! Legyen $E$ az origó, a négy csúcsba mutató vektor $\text{a}$, $\text{b}$, $\text{c}$, $\text{d}$ (2. ábra). $M$ helyvektora $\frac{\text{c}+\text{d}}{2}$ és $K$ helyvektora $\frac{\text{a}+\text{b}}{2}$, tehát $\begin{array}{c}{\displaystyle \overrightarrow{KM}=\frac{\text{c}+\text{d}}{2}-\frac{\text{a}+\text{b}}{2}=\frac{\text{d}-\text{a}}{2}+\frac{\text{c}-\text{b}}{2}\mathrm{.}}\end{array}$   2. ábra   Az $EN$ egyenes irányvektora az $\overrightarrow{AD}=\text{d}-\text{a}$ vektor ${90}^{\circ }$-os elforgatottja, az $EL$ egyenesé pedig a $\overrightarrow{CB}=\text{b}-\text{c}$ vektoré. ($\text{d}-\text{a}$  ${90}^{\circ }$-os elforgatottját jelölje ${\left(\text{d}-\text{a}\right)}^{90}$. Mindkettőt pozitív irányba forgatjuk.) $\begin{array}{c}{\displaystyle \overrightarrow{LN}=\overrightarrow{EN}-\overrightarrow{EL}=\alpha \cdot {\left(\text{d}-\text{a}\right)}^{90}-\beta \cdot {\left(\text{b}-\text{c}\right)}^{90}=\alpha \cdot {\left(\text{d}-\text{a}\right)}^{90}+\beta \cdot {\left(\text{c}-\text{b}\right)}^{90}\mathrm{,}}\end{array}$ ahol $\alpha \mathrm{,}\beta \in \text{R}$. Tehát ha $\alpha =\beta$, akkor az $\overrightarrow{LN}$ vektor valóban merőleges az $\overrightarrow{KM}$ vektorra. Azt kell tehát még belátnunk, hogy az $EN$ és $EL$ távolságok úgy aránylanak egymáshoz, mint a négyszög $AD$ és $CB$ oldalai. Mivel $ABCD$ húrnégyszög, $EDA\sphericalangle =BCE\sphericalangle$ és $EAD\sphericalangle =CBE\sphericalangle$, valamint nyilván $AED\sphericalangle =CEB\sphericalangle$. Így $EDA$ háromszög hasonló $ECB$-hez, vagyis $\begin{array}{c}{\displaystyle \alpha =\frac{EN}{AD}=\frac{EL}{CB}=\beta \mathrm{,}}\end{array}$ tehát igaz az arányokra vonatkozó állítás. Ezzel a feladat állítását beláttuk.