Kezdőlap


Feladat:	2014. évi Kürschák matematikaverseny 2. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Fleiner Tamás
Füzet:	2015/február, 69 - 70. oldal		PDF \| MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd), Síkgeometriai bizonyítások, Magasságvonal, Körülírt kör
Hivatkozás(ok):	Feladatok: 2015/február: 2014. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Jelölje az

A B C

A A_{1} A_{2}

B B_{1} B_{2}

és

C C_{1} C_{2}

köröket rendre

k

k_{a}

k_{b}

, illetve

k_{c}

; az

A B C

háromszög magasságpontja legyen

M

. A feltétel szerint az

A B C

háromszög hegyesszögű, ezért az

A_{1}

B_{1}

C_{1}

M

pontok

k

belsejében vannak.
A

k

kerületén az

A A_{2}

B B_{2}

és

C C_{2}

pontpárok páronként elválasztják egymást, ezért a

k_{a}

k_{b}

és

k_{c}

körök közül bármelyik kettő metszi egymást úgy, hogy az egyik metszéspontjuk

k

belsejében, a másik metszéspontjuk

k

-n kívül helyezkedik el. Legyen a

k_{a}

és a

k_{b}

körök metszéspontja

k

belsejében

X

, a másik metszéspontjuk legyen

Y

. Azt fogjuk megmutatni, hogy a

k_{c}

kör is átmegy az

X

és

Y

pontok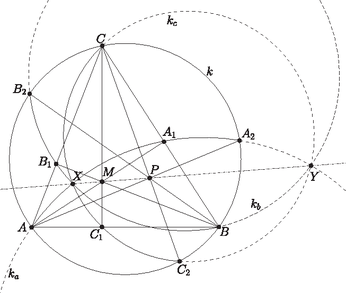on.

P

pont

k

-ra vonatkozó hatványa

\begin{matrix} P A \cdot P A_{2} = P B \cdot P B_{2} = P C \cdot P C_{2} . \end{matrix}

Ezek a szorzatok egyben a

P

hatványai a

k_{a}

k_{b}

, illetve

k_{c}

körökre. Tehát a

P

pontnak a

k_{a}

k_{b}

és

k_{c}

körökre vonatkozó hatványa ugyanakkora.
Hasonlóan, az

M

pontnak az

A B A_{1} B_{1}

B C B_{1} C_{1}

C A C_{1} A_{1}

körökre vonatkozó hatványa

\begin{matrix} M A \cdot M A_{1} = M B \cdot M B_{1} = M C \cdot M C_{1} . \end{matrix}

Ezek a szorzatok pedig az

M

hatványai a

k_{a}

k_{b}

, illetve

k_{c}

körökre. Tehát az

M

pontnak a

k_{a}

k_{b}

és

k_{c}

körökre vonatkozó hatványa is ugyanakkora.
A feltétel szerint

P

és

M

különböző. Így a

P M

egyenes a

k_{a}

k_{b}

és

k_{c}

körök közös hatványvonala. A három kör tehát egy körsorhoz tartozik, így

k_{a}

és

k_{b}

metszéspontjain átmegy

k_{c}

is.
Ezzel megmutattuk, hogy a

k_{a}

k_{b}

, illetve

k_{c}

körök

k

-n belüli ívei, nevezetesen az

A A_{1} A_{2}

B B_{1} B_{2}

és

C C_{1} C_{2}

körívek egy ponton mennek át.

□

Megjegyzés. Egy alkalmas sztereografikus projekcióval (térbeli inverzióval) visszavezethetjük az állítást arra a jól ismert tényre, hogy a gömbfelületen bármely három körvonal páronként vett hatványvonalai egy átmérőre illeszkednek.
Jelöljük

Π

-vel az

A B C

háromszög síkját, és legyen

Γ

az a gömb, amelynek a

k

főköre. A

P

pontban állítsunk merőleges egyenest

Π

-re; legyen ennek egyik döféspontja a

Γ

-val

O

. Invertáljuk az ábrát az

O

középpontú,

P

-n átmenő gömbre; a szokásos módon tetszőleges

x

objektum képét jelöljük

x'

-vel. Az inverzió jól ismert tulajdonságai szerint a

Π

sík képe az

O P

átmérőjű

Π'

gömb; a

Π

síkban fekvő körök képei a gömbfelületen fekvő körvonalak. Speciálisan, a

B C B_{1} C_{1}

, a

C A C_{1} A_{1}

és az

A B A_{1} B_{1}

körök képei a

B' C' B_{1}' C_{1}'

, a

C' A' C_{1}' A_{1}'

és az

A' B' A_{1}' B_{1}'

körvonalak.
A

Γ

gömb definíciója szerint a

Π

sík és a

Γ

gömb merőlegesen metszi egymást a

k

kör mentén. Mivel az inverzió szögtartó, az

Γ'

sík és a

Π'

gömb is merőlegesen metszi egymást a

k'

kör mentén, így

k'

Π'

gömbnek főköre.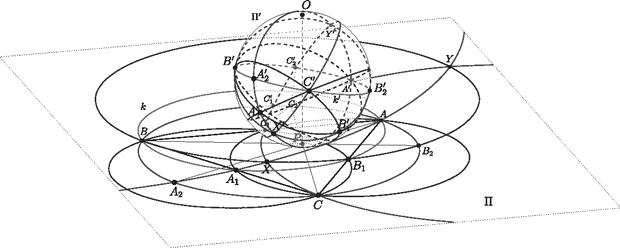

Vegyük észre, hogy az

A'

és

A_{2}'

pontokon a

Π'

gömbnek legalább két különböző főköre is átmegy: ilyen a

k'

kör, és az

O A' P A_{2}'

kör is. (Utóbbi átmegy az átellenes

O

és

P

pontokon, de nem szerepel az ábrán.) Ebből következik, hogy a

Π'

gömbön

A'

és

A_{2}'

átellenes pontok, és az

A' A_{1}' A_{2}'

körvonal is főkör. Ez a főkör átmegy a

C' A' C_{1}' A_{1}'

és az

A' B' A_{1}' B_{1}'

körök metszéspontjain,

A'

-n és

A_{1}'

-n; tehát az

A' A_{1}' A_{2}

körvonal nem más, mint a

C' A' C_{1}' A_{1}'

és az

A' B' A_{1}' B_{1}'

körök hatványvonala.
Hasonlóan kapjuk, hogy a

B' C' B_{1}' C_{1}'

és az

A' B' A_{1}' B_{1}'

kör hatványvonala a

B' B_{1}' B_{2}'

főkör, illetve hogy a

B' C' B_{1}' C_{1}'

és az

C' A' C_{1}' A_{1}'

kör hatványvonala a

C' C_{1}' C_{2}'

főkör.
A három hatványvonal két, egymással átellenes közös ponton megy át; jelölje ezeket

X'

és

Y'

úgy, hogy

X

és

O

k'

főkör ellentétes oldalán legyenek. Az

X'

Y'

pontokat

O

-ból visszavetítve a

Π

síkra, megkapjuk az

A A_{1} A_{2}

B B_{1} B_{2}

, és

C C_{1} C_{2}

körök közös pontjait: az

X

pont a

k

körön belül, az

Y

pont a

k

körön kívül lesz.