Feladat:	B.4671	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Andó Angelika ,  Baran Zsuzsanna ,  Bodolai Előd ,  Cseh Kristóf ,  Csépai András ,  Döbröntei Dávid Bence ,  Fekete Panna ,  Gál Boglárka ,  Glattfelder Hanna ,  Hansel Soma ,  Kocsis Júlia ,  Kovács Péter Tamás ,  Nagy Dávid Paszkál ,  Németh Balázs ,  Papp Marcell ,  Polgár Márton ,  Schrettner Bálint ,  Schwarz Tamás ,  Szebellédi Márton ,  Szécsényi Nándor ,  Tomcsányi Gergely ,  Tóth Viktor ,  Varga-Umbrich Eszter ,  Williams Kada
Füzet:	2015/december, 534 - 536. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Egyéb sokszögek geometriája, Síkgeometriai bizonyítások, Hasonlósági transzformációk
Hivatkozás(ok):	Feladatok: 2014/december: B.4671

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Legyen az $A{B}_1{B}_2\text{...}{B}_6$ hétszög körülírt köre $k_B$, az $A{C}_1{C}_2\text{...}{C}_6$ hétszög körülírt köre pedig $k_C$. A $k_B$ és $k_C$ körök átmennek $A$-n. Jelölje a két kör $A$-tól különböző metszéspontját $M$ (ha a két kör $A$-ban érinti egymást, akkor $M\equiv A$). Megmutatjuk, hogy $i=\mathrm{1,2,}\text{...}\mathrm{,6}$ esetén a $B_i{C}_i$ egyenesek mindegyike átmegy $M$-en. Legyen $\alpha =\frac{{180}^{\circ }}{7}$. Ez a szabályos hétszögek oldalaihoz tartozó kerületi szög mind a $k_B$, mind pedig a $k_C$ körben. Az $\alpha$ szög segítségével meg fogjuk határozni az $AM{B}_i$ és $AM{C}_i$ szögeket. Két fő esetet különböztetünk meg, annak megfelelően, hogy a $B_i$ és $C_i$ csúcsok az $AM$ egyenes (ha a két kör $A$-ban érinti egymást, akkor az $A$-beli közös érintőjük) által meghatározott két félsík közül ugyanabba vagy különbözőekbe esnek. Feltehetjük, hogy a hétszögek pozitív körüljárásúak. Nevezzük az $AM$ egyenes által meghatározott félsíkok közül pozitívnak azt, amelyik a $k_B$ és $k_C$ körök $A$-ból $M$-be menő ívei közül a pozitív irányút tartalmazza, negatív félsíknak pedig a másikat, s jelölje e nyílt félsíkokat ${\text{F}}_{+}$ és ${\text{F}}_{-}$ (1. ábra). Ekkor a kerületi szögek tételét alkalmazva kapjuk, hogy 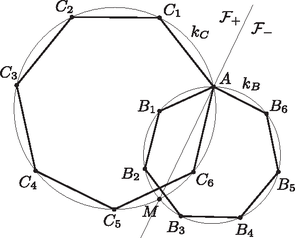$\begin{array}{c}{\displaystyle AM{B}_i\sphericalangle =\{{\displaystyle \begin{array}{cc}\hfill {\displaystyle AM{B}_1\sphericalangle +B_{1}M{B}_2\sphericalangle +\text{...}+B_{i-1}M{B}_i\sphericalangle =i\alpha \mathrm{,}}& {\displaystyle \text{ha }{B}_i\in {\text{F}}_{+}\mathrm{,}}\hfill \\ \hfill {\displaystyle AM{B}_6\sphericalangle +B_{6}M{B}_5\sphericalangle +\text{...}+B_{i+1}M{B}_i\sphericalangle =\left(7-i\right)\alpha \mathrm{,}}& {\displaystyle \text{ha }{B}_i\in {\text{F}}_{-}\mathrm{,}}\hfill \end{array}}}\end{array}$ s ugyanígy $\begin{array}{c}{\displaystyle AM{C}_i\sphericalangle =\{{\displaystyle \begin{array}{cc}\hfill {\displaystyle i\alpha \mathrm{,}}& {\displaystyle \text{ha }{C}_i\in {\text{F}}_{+}\mathrm{,}}\hfill \\ \hfill {\displaystyle \left(7-i\right)\alpha \mathrm{,}}& {\displaystyle \text{ha }{C}_i\in {\text{F}}_{-}\mathrm{.}}\hfill \end{array}}}\end{array}$   1. ábra   Ezek után már egyszerűen beláthatjuk, hogy az $M$, $B_i$ és $C_i$ pontok minden $i=\mathrm{1,2,}\text{...}\mathrm{,6}$ esetén egy egyenesbe esnek. Ha $M\equiv B_i$ vagy $M\equiv C_i$, akkor ez nyilvánvaló. Ha $B_i$ és $C_i$ közül mindkettő az ${\text{F}}_{+}$ vagy az ${\text{F}}_{-}$ félsíkba esik, akkor $AM{B}_i\sphericalangle =AM{C}_i\sphericalangle$, és mivel $B_i$ és $C_i$ az $AM$ egyenesnek ugyanazon az oldalán vannak, ezért ebből következik, hogy $B_i$ és $C_i$ ugyanazon az $M$-ből kiinduló félegyenesen helyezkednek el (2. ábra). Ha viszont $B_i$ és $C_i$ különböző félsíkokban vannak, akkor 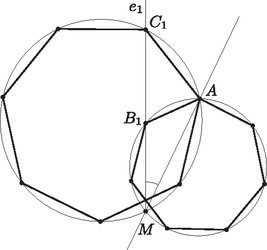$\begin{array}{c}{\displaystyle AM{B}_i\sphericalangle +AM{C}_i\sphericalangle =i\cdot \alpha +\left(7-i\right)\cdot \alpha ={180}^{\circ }\mathrm{,}}\end{array}$ s mivel $B_i$ és $C_i$ az $AM$ egyenesnek különböző oldalain vannak, ezért ebből következik, hogy $B_i$, $C_i$ és $M$ kollineárisak (3. ábra).   2. ábra 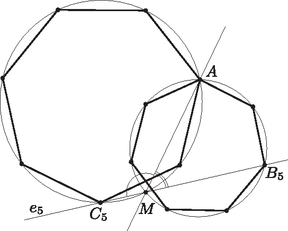    3. ábra   Az előző bekezdésben leírtak $M\equiv A$ esetén is igazak, csak azt kell meggondolnunk, hogy ekkor $AM{B}_i\sphericalangle$ és $AM{C}_i\sphericalangle$ a megfelelő érintőszárú kerületi szögeket jelöli (4. és 5. ábra). 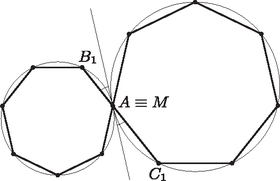  4. ábra 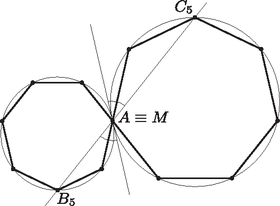    5. ábra   Ezzel a feladat állítását beláttuk.   Megjegyzés. A megoldás során nem használtuk ki, hogy a sokszögek oldalszáma 7. Ugyanezzel a gondolatmenettel belátható az állítás tetszőleges $n$-szögekre is. Sőt tulajdonképpen azt bizonyítottuk be, hogy ha tekintjük az egymást az $A$ pontban metsző $k_B$ és $k_C$ körvonalak azon $B_{\phi }$ és $C_{\phi }$ pontjait, melyekre az ugyanolyan irányítású $A{B}_{\phi }$ és $A{C}_{\phi }$ ívekhez tartozó középponti szögek megegyeznek, akkor a $B_{\phi }{C}_{\phi }$ egyenesek átmennek $k_B$ és $k_C$ másik (esetleg $A$-val egybeeső) metszéspontján.