Feladat:	2015. évi Nemzetközi Matematika Diákolimpia 21. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Baran Zsuzsanna
Füzet:	2015/október, 390. oldal		PDF  |  MathML
Témakör(ök):	Nemzetközi Matematikai Diákolimpia, Síkgeometriai bizonyítások, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 2015/szeptember: 2015. évi Nemzetközi Matematika Diákolimpia 21. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Baran Zsuzsanna megoldása. Először belátom, hogy $BGE\sphericalangle =DFC\sphericalangle$. $BCF\sphericalangle \left(=DCF\sphericalangle \right)=BGF\sphericalangle$, mert $\Omega$ körnek azonos ívén nyugvó kerületi szögek. Az $FCD$ háromszögben $DFC\sphericalangle +DCF\sphericalangle +FDC\sphericalangle ={180}^{\circ }$. Mivel $FDEG$ húrnégyszög, az is igaz, hogy $FDE\sphericalangle +FGE\sphericalangle =FDE\sphericalangle +BGF\sphericalangle +BGE\sphericalangle ={180}^{\circ }$. Ezek szerint 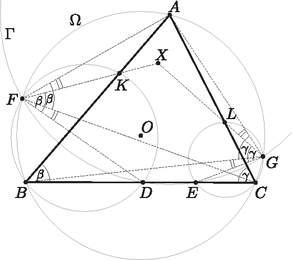$DFC\sphericalangle ={180}^{\circ }-DCF\sphericalangle -FDC\sphericalangle ={180}^{\circ }-BGF\sphericalangle -FDE\sphericalangle =BGE\sphericalangle$.     A kerületi szögek tétele miatt az is igaz, hogy ${\displaystyle \begin{array}{cc}\hfill {\displaystyle DFK\sphericalangle }& {\displaystyle =DBK\sphericalangle \text{ (<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi><mi>D</mi><mi>K</mi></math> kör <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi><mi>K</mi></math> ívén nyugszanak)}=}\hfill \\ \hfill {\displaystyle =CBA\sphericalangle }& {\displaystyle =CFA\sphericalangle \text{ (<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Ω</mi></math> <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mi>C</mi></math> ívén nyugszanak),}}\hfill \\ \hfill {\displaystyle EGL\sphericalangle }& {\displaystyle =ECL\sphericalangle \text{ (<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi><mi>E</mi><mi>L</mi></math> kör <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi><mi>L</mi></math> ívén nyugszanak)}=}\hfill \\ \hfill {\displaystyle =BCA\sphericalangle }& {\displaystyle =BGA\sphericalangle \text{ (<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Ω</mi></math> <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mi>B</mi></math> ívén nyugszanak).}}\hfill \\ \hfill {\displaystyle AFK\sphericalangle }& {\displaystyle =AFD\sphericalangle -DFK\sphericalangle =AFD\sphericalangle -CFA\sphericalangle =DFC\sphericalangle =}\hfill \\ \hfill {\displaystyle }& {\displaystyle =BGE\sphericalangle =AGE\sphericalangle -BGA\sphericalangle =AGE\sphericalangle -EGL\sphericalangle =AGL\sphericalangle \mathrm{.}}\hfill \end{array}}$ Ezek szerint $AFX\sphericalangle =AFK\sphericalangle =AGL\sphericalangle =AGX\sphericalangle$. Az $AFG$ háromszög egyenlőszárú ($AF$ és $AG$ egyaránt $\Gamma$ sugarai), ezért $AFG\sphericalangle =AGF\sphericalangle$ és $A$ illeszkedik az $FG$ szakasz felezőmerőlegesére. $OF=OG$ ($\Omega$ sugarai), ezért $O$ is illeszkedik az $FG$ szakasz felezőmerőlegesére. Így az $AO$ egyenes az $FG$ szakasz felezőmerőlegese. $\begin{array}{c}{\displaystyle XFG\sphericalangle =|AFG\sphericalangle -AFX\sphericalangle |=|AGF\sphericalangle -AGX\sphericalangle |=XGF\sphericalangle \mathrm{.}}\end{array}$ Ezek szerint az $XFG$ háromszög egyenlőszárú, így az $X$ pont illeszkedik az $FG$ szakasz felezőmerőlegesére, azaz az $AO$ egyenesre. Ezt akartuk belátni. Mivel a feladatban megadták, hogy a pontok milyen sorrendben helyezkednek el a $BC$ szakaszon, illetve az $\Omega$ körön, diszkusszióra nincs szükség.