Feladat:	2015. évi Nemzetközi Matematika Diákolimpia 3. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Janzer Barnabás
Füzet:	2015/október, 389. oldal		PDF  |  MathML
Témakör(ök):	Síkgeometriai bizonyítások, Nemzetközi Matematikai Diákolimpia, Körülírt kör, Inverzió
Hivatkozás(ok):	Feladatok: 2015/szeptember: 2015. évi Nemzetközi Matematika Diákolimpia 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.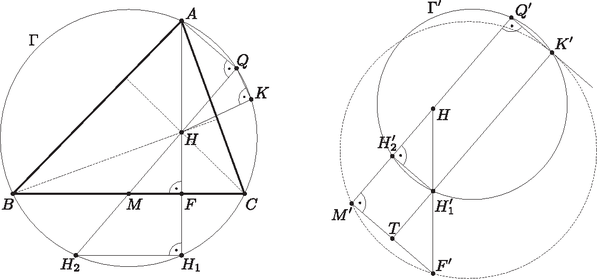   Janzer Barnabás megoldása. Legyen a $H$ pont tükörképe a $BC$ egyenesre (vagyis az $F$ pontra) $H_1$, az $M$ pontra $H_2$. Ismert, hogy $H_1$ és $H_2$ a $\Gamma$ körön vannak, továbbá $H_2$ az $A$-val átellenes pont. A Thalész-tétel megfordításából a $QH$ egyenes $\Gamma$-t az $A$-val átellenes pontban, vagyis $H_2$-ben metszi. Ezért $HQ$ és $HM$ is átmegy $H_2$-n, vagyis $H_2$, $M$, $H$ és $Q$ egy egyenesen vannak. Az $A$, $H$ és $H_1$ pontok egy egyenesen vannak, ezért a Thalész-tételből $H_2{H}_{1}H\sphericalangle ={90}^{\circ }$. Az $A$, $B$, $C$ pontokra a továbbiakban nincs szükségünk a megoldás során.     Invertáljunk $H$ középponttal. Ekkor $M\text{'}$, $H_2\text{'}$, $H$, $Q\text{'}$ ilyen sorrendben egy egyenesen vannak. $HQ$ Thalész-köre (melyen $K$ rajta van) egy $M\text{'}Q\text{'}$-re merőleges egyenesbe megy át (hiszen középpontja rajta van a $H_{2}MHQ$ egyenesen). Hasonlóan $HM$ és $H{H}_2$ Thalész-körének képe is egy $M\text{'}Q\text{'}$-re merőleges egyenes, előbbi körön $F$, utóbbin $H_1$ rajta van. Továbbá $H_2\text{'}$ és $H_1\text{'}$ rendre a $HM\text{'}$ és $HF\text{'}$ szakasz felezőpontja. $\Gamma \text{'}$ egy kör, mely áthalad a $Q\text{'}$, $H_2\text{'}$, $H_1\text{'}$, $K\text{'}$ pontokon. $Q\text{'}{H}_2\text{'}{H}_1\text{'}K\text{'}$ négyszög derékszögű trapéz és húrnégyszög egyben, ezért téglalap. Messe $K\text{'}{H}_1\text{'}$ egyenes $M\text{'}F\text{'}$-t a $T$ pontban. $M\text{'}F\text{'}H$-ban $H_1\text{'}T$ középvonal, mivel $H_1\text{'}$ felezőpont és $H_1\text{'}T$ párhuzamos $HM\text{'}$-vel. Ezért $T{H}_1\text{'}K\text{'}$ egyenes szakaszfelező merőlegese az $M\text{'}F\text{'}$ szakasznak, így a szimmetria miatt $M\text{'}F\text{'}K\text{'}$ körülírt köre érinti (az $M\text{'}F\text{'}$-vel párhuzamos) $Q\text{'}K\text{'}$ egyenest. Így ősképeik is érintik egymást, ami pont a bizonyítandó állítás.