Feladat:	2015. évi Nemzetközi Matematika Diákolimpia 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Di Giovanni Márk
Füzet:	2015/október, 386 - 387. oldal		PDF  |  MathML
Témakör(ök):	Nemzetközi Matematikai Diákolimpia, Ponthalmazok, Indirekt bizonyítási mód
Hivatkozás(ok):	Feladatok: 2015/szeptember: 2015. évi Nemzetközi Matematika Diákolimpia 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Di Giovanni Márk megoldása. $a)$ Ha $n$ páratlan, akkor tekintsünk egy szabályos $n$-szöget és lássuk be, hogy ez egy kiegyensúlyozott halmaz. Ehhez tekintsünk két tetszőleges, különböző $A$ és $B$ pontot és a távolságukat ívhosszban mérve (a sokszög körülírt köre mentén). Ekkor a két távolság (a hosszabb és rövidebb ív mentén) összege $n$, azaz páratlan, ezért az egyik távolság páratlan a másik pedig páros. Ha viszont az egyik ív hossza páros, akkor $S$ tartalmazza az ívfelezőpontot, ami ugyanakkora távolságra van $A$-tól és $B$-től. Ha $n$ páros, akkor tekintsünk egy kört és $S$ legyen a következő pontok halmaza: a kör $O$ középpontja és a kör kerületének néhány pontja az ábra szerint: $A$, $B$, $C$ úgy, hogy $ABCO$ rombusz legyen, továbbá tetszőleges $k$ darab pont $\left(P_1\mathrm{,}{P}_2\mathrm{,}\text{...}\mathrm{,}{P}_k\right)$, illetve ezen pontok $O$ körüli ${60}^{\circ }$-os pozitív iránybeli elforgatottja 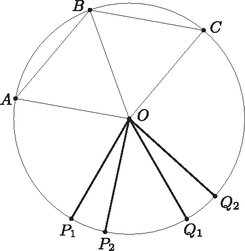$\left(Q_1\mathrm{,}{Q}_2\mathrm{,}\text{...}\mathrm{,}{Q}_k\right)$.     Nyilván megválaszthatjuk a $P_i$-pontokat úgy, hogy az összes általunk kiválasztott pont különböző legyen. Ekkor $S$-nek pontosan $2k+4$ darab eleme van (ahol $k$ tetszőleges nemnegatív egész). Tekintsünk most két különböző $S$-beli pontot. Ha mindkettő a kör kerületén van, akkor a kör középpontja egyenlő távol van tőlük. Ha az egyik a kör középpontja, akkor mivel $A$  $B$-nek, $B$  $C$-nek, illetve $Q_i$  $P_i$-nek a ${60}^{\circ }$-os elforgatottja, ezért a szabályos háromszögek miatt azonnal találunk olyan pontot, ami a két kiválasztott ponttól egyenlő távolságra van. Ezzel beláttuk, hogy $S$ kiegyensúlyozott. Továbbá $2k+4$ felveszi az összes 3-nál nagyobb páros számot. Tehát minden $n\ge 3$ egészre létezik $n$ elemű kiegyensúlyozott halmaz. $b)$ Azt állítjuk, hogy pontosan a páratlan $n$-ekre létezik $n$ elemű kiegyensúlyozott, centrum-nélküli halmaz. Ha $n$ páratlan, akkor a szabályos $n$-szög kiegyensúlyozott halmaz (ezt már korábban beláttuk), továbbá bármely három pontját is választjuk ki, az a pont, amely mindhármuktól egyenlő távolságra van, éppen a körülírt körük középpontja, ami nyilván megegyezik a szabályos $n$-szög körülírt körének középpontjával. Ez a pont viszont nem $S$-beli, tehát $S$ centrum-nélküli. Lássuk most be, hogy páros $n$-re nem létezik ilyen $S$ halmaz. Legyen $n=2k$ és tegyük fel indirekt, hogy találtunk ilyen $S$-et. Ekkor egy tetszőleges $A$ csúcshoz legfeljebb $k-1$ darab $S$-beli pontpár található úgy, hogy $A$ rajta legyen a felezőmerőlegesükön, mert ha létezne $k$ ilyen pár, akkor a $2k-1$ csúcs közül lenne olyan $B$ pont, amihez tartozó két felezőmerőlegesen is rajta lenne az $A$ pont. Tekintsük ezen felezőmerőlegeseket meghatározó szakaszokat: $BC$-t és $BD$-t. Ekkor $AB=AC$ és $AB=AD$-ből $AB=AC=AD$ következik, tehát $S$-nek van centruma, ami ellentmond eredeti feltevésünknek. Tehát $S$-nek minden csúcsa legfeljebb $k-1$ darab különböző $S$-beli pontpár által meghatározott felezőmerőlegesen lehet rajta. Viszont összesen $\left(\genfrac{}{}{0ex}{}{2k}{2}\right)=k\left(2k-1\right)$ darab pontpár van, amelyek mindegyikéhez tartozik egy felezőmerőleges, továbbá minden pontpár által meghatározott felezőmerőlegesen van legalább egy darab $S$-beli pont. Tehát $k\left(2k-1\right)\le 2k\left(k-1\right)$, azaz $k\ge 2k$, ami nyilvánvalóan ellentmondás. Így páros $n$-re nincsen kiegyensúlyozott, centrum-nélküli halmaz. Összefoglalva: pontosan a páratlan $n$-ekre létezik kiegyensúlyozott, centrum-nélküli $S$ halmaz.