Kezdőlap


Feladat:	2013. évi Nemzetközi Matematika Diákolimpia 21. feladata	Korcsoport: -	Nehézségi fok: -
Megoldó(k):	Fehér Zsombor
Füzet:	2013/október, 391 - 392. oldal		PDF \| MathML
Hivatkozás(ok):	Feladatok: 2013/szeptember: 2013. évi Nemzetközi Matematika Diákolimpia 21. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Fehér Zsombor megoldása. Miquel tétele szerint az $A B C$ háromszög $A B$ , $B C$ , $C A$ oldalegyenesein fekvő tetszőleges $N$ , $W$ , $M$ pontokra a $B W N$ , $C M W$ , és $A N M$ körök egy pontban metszik egymást. Ezt bebizonyíthatjuk a következőképpen:
Legyen a $B W N$ és $C M W$ körök második metszéspontja $P$ . Húrnégyszögben a szemközti szögek összege $180^{\circ}$ , így ha $P$ az $A B C$ háromszög belső pontja, akkor

\begin{matrix} M P N ∢ = 360^{\circ} - N P W ∢ - W P M ∢ = W B N ∢ + M C W ∢ = 180^{\circ} - B A C ∢ . \end{matrix}

Tehát

M P N ∢ = 180^{\circ} - N A M ∢

alapján

A N P M

is húrnégyszög. Irányított szögekkel számolva az előbbi bizonyítás működik akkor is, ha

P

külső pont.

B N C ∢ = B M C ∢ = 90^{\circ}

miatt a

B

N M

C

pontok egy körön vannak, legyen ez a kör

ω_{3}

. Ekkor az

ω_{1}

ω_{2}

és

ω_{3}

körök hatványvonalai egy ponton mennek át, tehát a

W P

egyenes átmegy

B N

és

C M

metszéspontján, az

A

ponton. Mivel

H N A ∢ = H M A ∢ = 90^{\circ}

, ezért

H

is rajta van az

A N M

körön, így

H P A ∢ = H M A ∢ = 90^{\circ}

. Amennyiben

H = P

, akkor a

H P

egyenest értelmezzük az

A N H P M

kör

H

-beli érintőjének.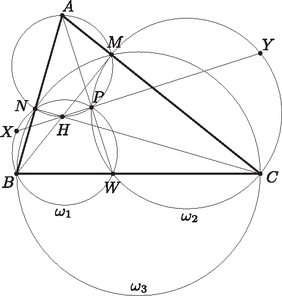

Mivel

W X

és

W Y

átmérő

ω_{1}

-ben és

ω_{2}

-ben, azért

W P X ∢ = W P Y ∢ = 90^{\circ}

. Ez pedig azt jelenti, hogy a

H

X

Y

pontok mind rajta vannak a

W A

-ra

P

-ben állított merőleges egyenesen.