Kezdőlap


Feladat:	2013. évi Nemzetközi Matematika Diákolimpia 13. feladata	Korcsoport: -	Nehézségi fok: -
Megoldó(k):	Szabó Attila
Füzet:	2013/október, 388 - 391. oldal		PDF \| MathML
Hivatkozás(ok):	Feladatok: 2013/szeptember: 2013. évi Nemzetközi Matematika Diákolimpia 13. feladata

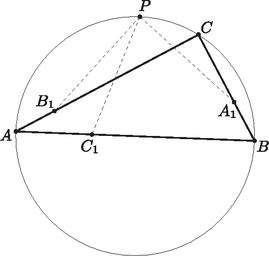
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Szabó Attila megoldása. Az általánosság megszorítása nélkül feltehetjük, hogy az $A_{1} B_{1} C_{1}$ kör $P$ középpontja a körülírt kör $B$ -t nem tartalmazó $A C$ ívén van. A háromszög oldalait és szögeit a szokásos módon jelöljük, félkerülete $s$ , területe $t$ , beírt és körülírt körének sugara rendre $ϱ$ és $R$ . Legyenek a $P A$ , $P B$ , $P C$ szakaszok látószögei rendre $P B A ∢ = P C A ∢ = α'$ , $P C B ∢ = π - P A B ∢ = β'$ és $P A C ∢ = P B C ∢ = γ'$ . Ekkor a szinusztétel miatt

\begin{matrix} P A = 2 R sin α', P B = 2 R sin β', P C = 2 R sin γ', \end{matrix}

(1)

a következő összefüggések egyszerű szögszámolással adódnak:

\begin{matrix} π - β' = α + γ', β = α' + γ', β' = γ + α' . \end{matrix}

(2)

Ismert továbbá, hogy

C B_{1} = B C_{1} = s - a

A C_{1} = C A_{1} = s - b

A B_{1} = B A_{1} = s - c

.
Írjuk fel a koszinusztételt a

B_{1} C P

és

C_{1} B P

háromszögekben:

\begin{matrix} P B_{1}^{2} & = {(s - a)}^{2} + C P^{2} - 2 (s - a) C P cos α'; & (3) \\ P C_{1}^{2} & = {(s - a)}^{2} + B P^{2} - 2 (s - a) B P cos α' . & (4) \end{matrix}

Mivel

P B_{1} = P C_{1}

, a két jobb oldal egyenlő:

\begin{matrix} C P^{2} - 2 (s - a) C P cos α' = B P^{2} - 2 (s - a) B P cos α', \\ (C P - B P) (C P + B P) = C P^{2} - B P^{2} = 2 (s - a) (C P - B P) cos α' . & (5) \end{matrix}

B_{1} A P

és

A_{1} B P

háromszögekben felírt koszinusztételekből ugyanígy következik, hogy

\begin{matrix} (A P - B P) (A P + B P) = 2 (s - c) (A P - B P) cos γ' . \end{matrix}

(6)

Az (5), (6) egyenletek

C P = B P

, illetve

A P = B P

esetén is teljesülnek. Ha viszont mindkettő teljesülne,

P

A B C

kör középpontja lenne, ami ellentmondás: az általánosság megszorítása nélkül feltehető, hogy

C P \neq B P

. Ekkor (5) mindkét oldalát eloszthatjuk

(C P - B P)

-vel:

\begin{matrix} C P + B P = 2 (s - a) cos α', & (7) \\ 2 R (sin γ' + sin β') = (b + c - a) cos α' = 2 R (sin β + sin γ - sin α) cos α', \\ sin (β - α') + sin (γ + α') = (sin β + sin γ - sin α) cos α', \\ sin β cos α' - cos β sin α' + sin γ cos α' + cos γ sin α' = \\ = sin β cos α' + sin γ cos α' - sin α cos α', \\ sin α cos α' = sin α' (cos β - cos γ), \\ ctg α' = \frac{cos β - cos γ}{sin α} . & (8) \end{matrix}

Most írjuk fel a koszinusztételt az

A_{1} C P

és

A C_{1} P

háromszögekben is:

\begin{matrix} P A_{1}^{2} & = {(s - b)}^{2} + P C^{2} - 2 (s - b) P C cos β'; & (9) \\ P C_{1}^{2} & = {(s - b)}^{2} + P A^{2} + 2 (s - b) P A cos β' . & (10) \end{matrix}

P A_{1} = P C_{1}

miatt a két jobb oldal egyenlő:

\begin{matrix} P C^{2} - 2 (s - b) P C cos β' = P A^{2} + 2 (s - b) P A cos β', & (11) \\ (P C - P A) (P C + P A) = P C^{2} - P A^{2} = 2 (s - b) (P A + P C) cos β', \\ P C - P A = 2 (s - b) cos β', \\ 2 R (sin γ' - sin α') = (a + c - b) cos β' = 2 R (sin α + sin γ - sin β) cos β', \\ sin (β' + α) - sin (β' - γ) = (sin α + sin γ - sin β) cos β', \\ sin β' cos α + cos β' sin α - sin β' cos γ + cos β' sin γ = \\ = sin α cos β' + sin γ cos β' - sin β cos β', \\ sin β' (cos γ - cos α) = sin β cos β', \\ ctg β' = \frac{cos γ - cos α}{sin β} . & (12) \end{matrix}

(2) miatt

β' - α' = γ

: ha ez teljesül, ugyanez fennáll kotangenseikre is, azaz

ctg (β' - α') = ctg γ

. Felhasználva a kotangens addíciós képletét (nullával osztás nem fordul elő, mivel

0 < γ < π

\begin{matrix} \frac{cos γ}{sin γ} & = ctg γ = \frac{ctg α' ctg β' + 1}{ctg α' - ctg β'} = \frac{\frac{cos β - cos γ}{sin α} \frac{cos γ - cos α}{sin β} + 1}{\frac{cos β - cos γ}{sin α} - \frac{cos γ - cos α}{sin β}} = \\ = \frac{(cos β - cos γ) (cos γ - cos α) + sin α sin β}{(cos β - cos γ) sin β - (cos γ - cos α) sin α} = \\ = \frac{- cos β cos α + sin β sin α - cos^{2} γ + cos α cos γ + cos β cos γ}{sin α cos α + sin β cos β - sin α cos γ - sin β cos γ} = \\ = \frac{- cos (α + β) + cos γ (cos α + cos β - cos γ)}{\frac{1}{2} (sin 2 α + sin 2 β) - cos γ (sin α + sin β)} = \\ = \frac{cos γ (1 + cos α + cos β - cos γ)}{sin (α + β) cos (α - β) - cos γ (sin α + sin β)} = \\ = \frac{cos γ (1 + cos α + cos β - cos γ)}{sin γ cos (α - β) - cos γ (sin α + sin β)} . \end{matrix}

A bizonyítandóból tehát következik a következő egyenlet teljesülése:

\begin{matrix} \frac{cos γ}{sin γ} = \frac{cos γ (1 + cos α + cos β - cos γ)}{sin γ cos (α - β) - cos γ (sin α + sin β)} . \end{matrix}

(13)

(13) nyilván igaz akkor, ha

cos γ = 0

, azaz

γ

derékszög. Tegyük fel most, hogy

γ

nem derékszög, azaz oszthatunk

cos γ

-val: ezt elvégezve és felszorozva a nevezőkkel:

\begin{matrix} sin γ cos (α - β) - cos γ (sin α + sin β) = sin γ (1 + cos α + cos β - cos γ), \\ sin γ cos (α - β) = sin γ + (sin γ cos α + cos γ sin α) + \\ + (sin γ cos β + cos γ sin β) - sin γ cos γ = \\ = sin γ + sin (γ + α) + sin (γ + β) - sin γ cos γ = \\ = sin γ + sin β + sin α + sin γ cos (α + β), \\ sin γ (cos (α - β) - cos (α + β)) = sin α + sin β + sin γ, \\ sin γ \cdot 2 sin α sin β = sin α + sin β + sin γ . \end{matrix}

Az egyenlet mindkét oldalát beszorozzuk

R^{2}

-tel és alkalmazzuk a szinusztételt:

\begin{matrix} t = \frac{1}{2} a b sin γ = \frac{R}{2} (a + b + c) = R s; \end{matrix}

másrészt viszont ismert módon

t = ϱ s

és nyilván

R > ϱ

: ezek együtt ellentmondásra vezetnek, a háromszög tehát

C

-ben derékszögű. Ezt kellett bizonyítani.

Megjegyzés. Nem tettük fel, hogy

A P \neq B P

. Ha a háromszög

C

-ben derékszögű, valóban

\begin{matrix} ctg α' = \frac{cos β}{sin α} = 1 = \frac{cos α}{sin β} = ctg β', \end{matrix}

tehát

α' = β'

, így

A P = B P

. Az tehát, hogy a háromszögnek

C

-ben kell derékszögűnek lennie, az általánosság megszorításaiból (

P

elhelyezéséből és

C P \neq B P

feltevéséből) következik.