Kezdőlap


Feladat:	C.998	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Póta Kristóf , Weimann Richárd
Füzet:	2010/szeptember, 332 - 333. oldal		PDF \| MathML
Témakör(ök):	C gyakorlat, Thalesz tétel és megfordítása, Mértani középtételek derékszögű háromszögekben, Tengelyes tükrözés, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 2009/szeptember: C.998

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen $A B = B C = x$ , $C D = y$ . Elegendő belátni, hogy a $P L Q$ háromszög $L$ -nél derékszögű, mert akkor $L$ rajta van $P Q$ Thalész-körén (szimmetria miatt $K$ i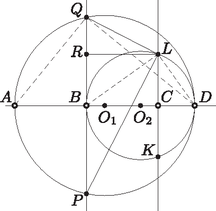s).

Állítsunk

L

-ből merőlegest

P Q

-ra, a talppontja legyen

R

. A

B D L

háromszög derékszögű, az átfogóhoz tartozó magasság

C L

. A derékszögű háromszögben felírva a magasságtételt:

\begin{matrix} C L = \sqrt[]{B C \cdot C D} = \sqrt[]{x y} = R B . \end{matrix}

A Q D

derékszögű háromszögben felírva a magasságtételt:

\begin{matrix} B Q = \sqrt[]{A B \cdot B D} = \sqrt[]{x (x + y)}; \end{matrix}

és innen

\begin{matrix} Q R & = B Q - R B = \sqrt[]{x (x + y)} - \sqrt[]{x y}, \\ R P & = B Q + R B = \sqrt[]{x (x + y)} + \sqrt[]{x y} . \end{matrix}

Mivel

\begin{matrix} Q R \cdot R P = (\sqrt[]{x (x + y)} - \sqrt[]{x y}) (\sqrt[]{x (x + y)} + \sqrt[]{x y}) = x (x + y) - x y = x^{2} = R L^{2}, \end{matrix}

így

R L = \sqrt[]{Q R \cdot R P}

, és a magasságtétel megfordítása miatt a

P Q L

háromszög derékszögű (a

P K Q

háromszög is derékszögű).
Ezzel igazoltuk az állítást.
II. megoldás. Az ábra jelölései szerint:

d_{A B} = d_{B C} = a

d_{C D} = b

. A

k_{1}

kör

A D

átmérőjű Thalész-kör, ezért

A P D ∢ = 90^{\circ}

. A

k_{2}

kör

B D

átmérőjű Thalész-kör, ezért

B K D ∢ = 90^{\circ}

. A

B K D

derékszögű háromszögben a befogótételt felírva:

\begin{matrix} d_{B K} = \sqrt[]{a (a + b)} . \end{matrix}

(1)

A D P

derékszögű háromszögben a magasságtételt alkalmazva:

\begin{matrix} d_{P B} = \sqrt[]{a (a + b)} . \end{matrix}

(2)

(1)-ből és (2)-ből következik:

d_{P B} = d_{B K}

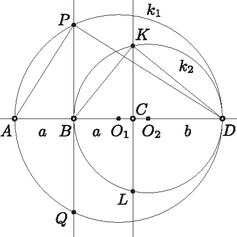A tengelyes szimmetria miatt

d_{B P} = d_{B Q}

és

d_{C K} = d_{C L}

, ezért a

P

K

L

Q

pontok a

B

ponttól egyenlő távolságra vannak, azaz illeszkednek a

B

középpontú

\sqrt[]{a (a + b)}

sugarú körvonalra, és ezt kellett bizonyítani.