Kezdőlap


Feladat:	C.991	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Nagy Bianka
Füzet:	2010/szeptember, 331 - 332. oldal		PDF \| MathML
Témakör(ök):	C gyakorlat, Érintőnégyszögek, Alakzatok hasonlósága, Elsőfokú (és arra visszavezethető) egyenletek
Hivatkozás(ok):	Feladatok: 2009/május: C.991

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Az átfogóra merőleges egyenesek kétféle esetet határoznak meg. Két különböző oldalhosszúságú érintőnégyszög és derékszögű háromszög jön létre. A két esetet külön kell vizsgálni.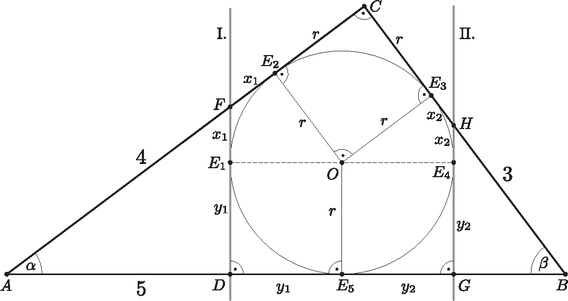

I. eset: A háromszög területét kétféleképpen felírva számítsuk ki az

A B C

háromszög beírható körének

r

sugarát:

\begin{matrix} T_{A B C} & = \frac{4 \cdot 3}{2} = 6. \\ T & = r \cdot s = r \cdot \frac{3 + 4 + 5}{2} = r \cdot 6 = 6, \end{matrix}

vagyis

r = 1

, és ekkor

y_{1} = 1

. Mivel az

E_{1}

E_{2}

E_{3}

E_{4}

E_{5}

érintési pontokba húzott sugár merőleges az érintőre, illetve a metsző egyenes merőleges az átfogóra, így a

D E_{5} O E_{1}

négyszög négyzet. Az

E_{2} O E_{3} C

négyszög szintén négyzet, így

E_{2} C = r

\begin{matrix} A F = 4 - x_{1} - r = 4 - x_{1} - 1 = 3 - x_{1} . \end{matrix}

A B C

háromszögből:

sin α = \frac{3}{5}

. Az

A F D

háromszögre:

\begin{matrix} sin α = \frac{3}{5} = \frac{x_{1} + y_{1}}{A F} = \frac{x_{1} + 1}{4 - r - x_{1}} = \frac{x_{1} + 1}{3 - x_{1}}; x_{1} = \frac{1}{2} . \end{matrix}

A négyszög oldalai:

\begin{matrix} F C = \frac{1}{2} + 1 = \frac{3}{2}, F D = \frac{1}{2} + 1 = \frac{3}{2}, C B = 3. \end{matrix}

Az érintőnégyszög tétel szerint:

\begin{matrix} D B + F C = C B + F D, azaz D B + \frac{3}{2} = 3 + \frac{3}{2}, így D B = 3. \end{matrix}

II. eset: Értelemszerűen a beírható kör sugara és

y

értéke sem változik:

y_{1} = y_{2} = 1

. Tehát:

B H = 3 - x_{2} - 1 = 2 - x_{2}

, és

sin β = \frac{4}{5}

(az

A B C

háromszögből).
A

H G B

háromszögre:

\begin{matrix} sin β = \frac{4}{5} = \frac{x_{2} + 1}{2 - x_{2}}, x_{2} = \frac{1}{3} . \end{matrix}

A négyszög oldalai:

\begin{matrix} A C = 4, C H = r + x_{2} = 1 + \frac{1}{3} = \frac{4}{3}, H G = x_{2} + y_{2} = \frac{1}{3} + 1 = \frac{4}{3}, \end{matrix}

és így

A G = 4