Kezdőlap


Feladat:	2010. évi Nemzetközi Matematika Diákolimpia 21. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bodor Bertalan
Füzet:	2010/október, 390. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Körülírt kör, Körérintők
Hivatkozás(ok):	Feladatok: 2010/szeptember: 2010. évi Nemzetközi Matematika Diákolimpia 21. feladata

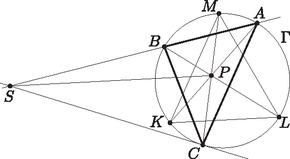
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Bodor Bertalan megoldása. Legyen $B A C ∢ = α$ , $A C B ∢ = β$ , $C B A ∢ = γ$ , $B S P ∢ = φ$ .
Az $S$ pontnak a $Γ$ körre vonatkozó hatványa

\begin{matrix} S A \cdot S B = S C^{2} = S P^{2} . \end{matrix}

Ebből

\frac{S B}{S P} = \frac{S P}{S A}

adódik, ami azt jelenti, hogy az

S B P

és

S P A

háromszögek hasonlóak egymáshoz. Ebből

S A P ∢ = S P B ∢

következik. Ekkor a kerületi szögek tételéből:

\begin{matrix} A K L ∢ & = A B L ∢ = B S P ∢ + S P B ∢ = φ + S P B ∢ = φ + S A P ∢ = \\ = φ + B A K ∢ = φ + B L K ∢, \end{matrix}

ahonnan

\begin{matrix} A K L ∢ - B L K ∢ = φ . \end{matrix}

(1)

Az érintő szárú kerületi szögek tétele miatt

B C S ∢ = C A B ∢ = α

. Az

A C S

háromszögben a szögek összege

180^{\circ} = α + A C S ∢ + C S P ∢ + A S P ∢ = 2 α + γ + φ + C S P ∢

, amiből

C S P ∢ = 180^{\circ} - 2 α - γ - φ

S C = S P

miatt az

S C P

háromszög egyenlő szárú, és akkor

\begin{matrix} S P C ∢ = S C P ∢ = \frac{180^{\circ} - C S P ∢}{2} = α + \frac{γ + φ}{2} . \end{matrix}

Ebből

\begin{matrix} B C M ∢ = S C P ∢ - B C S ∢ = \frac{γ + φ}{2} és A C M ∢ = \frac{γ - φ}{2} . \end{matrix}

A kerületi szögek tételéből:

\begin{matrix} B L M ∢ - A K M ∢ = B C M ∢ - A C M ∢ = \frac{γ + φ}{2} - \frac{γ - φ}{2} = φ . \end{matrix}

(2)

Az (1) és (2) egyenlőségek megfelelő oldalait egymásból kivonva

\begin{matrix} A K L ∢ - B L K ∢ - B L M ∢ + A K M ∢ = 0, \end{matrix}

azaz

\begin{matrix} A K L ∢ + A K M ∢ = B L K ∢ + B L M ∢ \Leftrightarrow M K L ∢ = M L K ∢ \Leftrightarrow M K = M L \end{matrix}

adódik, és ezt kellett bizonyítanunk.