Kezdőlap


Feladat:	2010. évi Nemzetközi Matematika Diákolimpia 12. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Nagy Donát
Füzet:	2010/október, 387 - 388. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Háromszög nevezetes körei
Hivatkozás(ok):	Feladatok: 2010/szeptember: 2010. évi Nemzetközi Matematika Diákolimpia 12. feladata

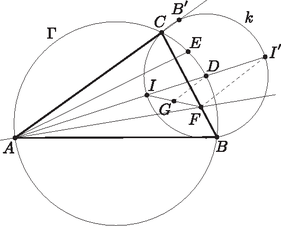
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Nagy Donát megoldása. Legyen $I$ tükörképe $D$ -re $I'$ , ekkor $I D = D I'$ , és így $G D ∥ F I'$ , hiszen $G D$ középvonal az $I F I'$ háromszögben. Mivel $A D$ szögfelező az $A B C$ háromszögben, a kerületi szögek tételéből $B D$ = $D C$ . Felhasználva, hogy $B I$ és $C I$ szögfelező az $A B C$ háromszögben

\begin{matrix} B I C ∢ & = 180^{\circ} - I C B ∢ - I B C ∢ = 180^{\circ} - \frac{A C B ∢}{2} - \frac{A B C ∢}{2}, továbbá \\ B D C ∢ & = 180^{\circ} - B A C ∢ = A B C ∢ + A C B ∢, \end{matrix}

hiszen

A B C D

húrnégyszög. A

D

középpontú

D B = D C

sugarú körön

I

rajta van, hiszen

B I C ∢ = 180^{\circ} - \frac{B D C ∢}{2}

, és

B C

elválasztja

D

-t és

I

-t. Az

I I'

nyilván ennek a

k

körnek az átmérője.

Legyen

F A I ∢ = I A E ∢ = φ

(a két szög a feladat feltétele és

I A B ∢ = I A C ∢

miatt egyenlő). A kerületi szögek tétele szerint

G D

és

E I

metszéspontja pontosan akkor van

Γ

-n, ha

\begin{matrix} (\vec{G D}, \vec{I E}) ∢ = φ = (\vec{A D}, \vec{A E}) ∢ = (\vec{A I'}, \vec{A E}) ∢ \end{matrix}

(itt a megfelelő vektorok által bezárt irányított szögek egyenlőségét tekintem). Mivel

\vec{G D}

és

\vec{F I'}

egyirányúak, ez ekvivalens azzal, hogy

\begin{matrix} (\vec{A I'}, \vec{A E}) ∢ = φ = (\vec{F I'}, \vec{I E}) ∢ . \end{matrix}

Tekintsük azt az

A

középpontú

φ

szögű nyújtva forgatást, ami

F

-et

I

-be viszi. Ez egy

φ

szöggel való nyújtva forgatás,

I'

képe az

A E

egyenesre,

A I'

képére esik, és a bizonyítandó ekvivalens azzal, hogy

F I'

képe

I E

, tehát hogy

I'

képe

E

. Az

I'

képe pontosan akkor

E

, ha

A F : A I = A I' : A E

, azaz

A E \cdot A F = A I \cdot A I'

.
Mivel

B A F ∢ = E A C ∢

és a kerületi szögek tételéből:

\begin{matrix} C E A ∢ = C B A ∢, A B F \sim A E C, A B : A F = A E : A C, A E \cdot A F = A B \cdot A C . \end{matrix}

Így az állítás pontosan akkor teljesül, ha

A B \cdot A C = A I \cdot A I'

. Legyen

B'

B

pont tükörképe

A D

-re; ekkor

B A D ∢ = D A C ∢

miatt

B'

A C

egyenesen van,

B D = B' D

miatt

B'

k

körön van, és

B' = C

(akkor és) csak akkor teljesül, ha

A B = A C

, de ekkor a kerületi szögek tételéből:

\begin{matrix} A C D ∢ = A C B ∢ + D A B ∢ = A C B ∢ + \frac{180^{\circ} - 2 A C B ∢}{2} = 90^{\circ}, \end{matrix}

így a

k

kör

B' = C

-ben érinti az

A C

egyenest. Ezekből következik, hogy

A

-nak a

k

-ra vonatkozó hatványa

A I \cdot A I' = A C \cdot A B' = A C \cdot A B

, és ezzel készen vagyunk.