Feladat:	4772. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csuha Boglárka ,  Gnädig Péter
Füzet:	2016/március, 178 - 181. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Hooke-törvény
Hivatkozás(ok):	Feladatok: 2015/november: 4772. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Jelöljük a feldarabolás után kapott rugók nyújtatlan hosszát ${\ell }_k$-val, a rugóállandóikat pedig $D_k$-val $\left(k=\mathrm{1,2,}\text{...}\mathrm{,}n\right)$. Az egyes rugódarabok rugóállandója fordítottan arányos a rugók hosszával, vagyis a megfelelő rugóhosszak és rugóállandók szorzata állandó: $\begin{array}{c}{\displaystyle {\ell }_1{D}_1={\ell }_2{D}_2=\text{...}={\ell }_n{D}_n=LD\mathrm{,}}\end{array}$ és így az egyes darabok rugóállandója kifejezhető az eredeti rugó adataival: $\begin{array}{c}{\displaystyle D_k=\frac{DL}{{\ell }_k}\left(k=\mathrm{1,2,}\text{...}\mathrm{,}n\right)\mathrm{.}}\end{array}$ $a)$ 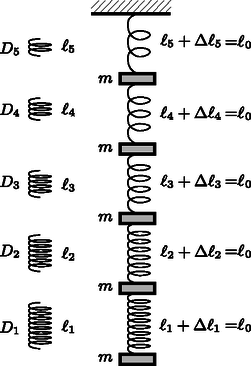Függesszük fel a rugókat és a nehezékeket a feladatban megadott módon, és számozzuk meg a rugókat lentről felfelé, ahogy azt az ábra mutatja.     A $k$-adik rugót az alatta lévő összes test súlya, tehát $k\cdot mg$ erő húzza, így a megnyúlása: $\begin{array}{c}{\displaystyle \Delta {\ell }_k=\frac{k\cdot mg}{D_k}=\frac{k\cdot mg}{DL}{\ell }_k=k\cdot {\ell }_k\mathrm{.}}\end{array}$ (Az utolsó lépésben kihasználtuk, hogy $DL=mg$.) A megnyúlt rugók hossza (a kialakuló egyensúlyi állapotban) azonos ${\ell }_0$ nagyságú, vagyis fennáll: $\begin{array}{c}{\displaystyle 2{\ell }_1=3{\ell }_2=4{\ell }_3=5{\ell }_4=6{\ell }_5\mathrm{.}}\end{array}$ Fejezzük ki ${\ell }_5$ segítségével a többi rugó nyújtatlan hosszát: $\begin{array}{c}{\displaystyle {\ell }_1=3{\ell }_5\mathrm{,}{\ell }_2=2{\ell }_5\mathrm{,}{\ell }_3=\frac{3}{2}{\ell }_5\mathrm{,}{\ell }_4=\frac{6}{5}{\ell }_5\mathrm{,}}\end{array}$ és mivel fennáll $\begin{array}{c}{\displaystyle {\ell }_1+{\ell }_2+{\ell }_3+{\ell }_4+{\ell }_5=\left(3+2+\frac{3}{2}+\frac{6}{5}+1\right){\ell }_5=\frac{87}{10}{\ell }_5=L\mathrm{,}}\end{array}$ a legfelső rugó hosszára ${\ell }_5=\frac{10}{87}L$ adódik. Hasonló módok kapjuk a többi rugódarab hosszát is: $\begin{array}{c}{\displaystyle {\ell }_1=\frac{30}{87}L\mathrm{,}{\ell }_2=\frac{20}{87}L\mathrm{,}{\ell }_3=\frac{15}{87}L\mathrm{,}{\ell }_4=\frac{12}{87}L\mathrm{.}}\end{array}$ Az eredeti rugót tehát ($n=5$ esetén) $30:25:15:12:10$ arányban kell feldarabolnunk, így érhetjük el, hogy a terhelés után a hosszuk ugyanakkora legyen. $b)$ A rendszer tömegközéppontja eddig a középső test tömegközéppontjával azonos helyen, a rugók felfüggesztésétől $3{\ell }_0=18{\ell }_1=\frac{60}{29}L$ távolságra volt. Ha most a rugósor alját $\delta$ távolsággal lehúzzuk, akkor mindegyik kis rugót feszítő erő ugyanakkora $F=D\delta$ értékkel növekszik, ennek hatására a megnyúlásuk valamekkora (rugónként különböző nagyságú) ${\delta }_k$ értékkel megnő. Felírhatjuk, hogy $\begin{array}{c}{\displaystyle F=D\delta =D_k{\delta }_k=\frac{DL}{{\ell }_k}{\delta }_k\mathrm{,}\text{vagyis}{\delta }_k=\frac{{\ell }_k}{L}\delta \mathrm{,}}\end{array}$ azaz $\begin{array}{c}{\displaystyle {\delta }_1=\frac{30}{87}\delta \mathrm{,}{\delta }_2=\frac{20}{87}\delta \mathrm{,}{\delta }_3=\frac{15}{87}\delta \mathrm{,}{\delta }_4=\frac{12}{87}\delta \mathrm{,}{\delta }_5=\frac{10}{87}\delta \mathrm{.}}\end{array}$ A rugók megnyúlásából kiszámíthatjuk, hogy mennyivel kerülnek mélyebbre az egyes testek: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \Delta h_5={\delta }_5=\frac{10}{87}\delta \mathrm{,}\Delta h_4={\delta }_5+{\delta }_4=\frac{22}{87}\delta \mathrm{,}\Delta h_3={\delta }_5+{\delta }_4+{\delta }_3=\frac{37}{87}\delta \mathrm{,}}\hfill \\ \hfill {\displaystyle \Delta h_2={\delta }_5+{\delta }_4+{\delta }_3+{\delta }_2=\frac{57}{87}\delta \mathrm{,}\Delta h_1={\delta }_5+{\delta }_4+{\delta }_3+{\delta }_2+{\delta }_1=\frac{87}{87}\delta =\delta \mathrm{.}}\hfill \end{array}}$ A felső két test tömegközéppontja $\begin{array}{c}{\displaystyle \Delta H_{\left(\mathrm{4,5}\right)}=\frac{\Delta h_5+\Delta h_4}{2}=\frac{16}{87}\delta }\end{array}$ távolsággal, az alső két test tömegközéppontja pedig $\begin{array}{c}{\displaystyle \Delta H_{\left(\mathrm{1,2}\right)}=\frac{\Delta h_1+\Delta h_2}{2}=\frac{72}{87}\delta }\end{array}$ távolsággal kerül mélyebbre, a négy testből álló, $4m$ tömegű alrendszer tömegközéppontjának elmozdulása $\begin{array}{c}{\displaystyle \Delta H_{\left(\mathrm{1,2,4,5}\right)}=\frac{H_{\left(\mathrm{1,2}\right)}+H_{\left(\mathrm{4,5}\right)}}{2}=\frac{44}{87}\delta \mathrm{.}}\end{array}$ Ha figyelembe vesszük még a középső ($m$ tömegű) test $\Delta h_3$ elmozdulását is, megkapjuk az egész rendszer tömegközéppontjának (amely $4:1$ arányban osztja az $m$ és a $4m$ tömegű részek közötti távolságot) keresett elmozdulását: $\begin{array}{c}{\displaystyle \Delta h_{\text{rendszer}}=\frac{4}{5}\Delta H_{\mathrm{1,2,4,5}}+\frac{1}{5}\Delta h_3=\frac{71}{145}\delta \approx 0\mathrm{,}49\delta \mathrm{.}}\end{array}$   II. megoldás. $b)$ A feladat második része a munkatétel segítségével is megoldható. Ha a legalsó testet $\delta$ távolsággal lejjebb húzzuk, az ehhez szükséges $F$ erő fokozatosan változik nulla és $D\delta$ között (hiszen a sorba kötött kis rugók együttese a szétdarabolás előtti, $D$ direkciós erejű rugóval egyenértékű). A lehúzáskor végzett $\begin{array}{c}{\displaystyle W=F_{\text{átlagos}}\delta =\frac{1}{2}D{\delta }^2}\end{array}$ munka egyrészt a rendszer helyzeti energiájának megváltozását, másrészt a rugók rugalmas energiájának növekedését fedezi: $\begin{array}{c}{\displaystyle W=\Delta E_{\text{helyzeti}}+\Delta E_{\text{rugalmas}}\mathrm{,}\text{ahol}\Delta E_{\text{helyzeti}}=-5mg\Delta h}\end{array}$ ($\Delta h$ a rendszer tömegközéppontjának keresett süllyedése), a rugók energiájának megváltozása pedig (az I. megoldás jelöléseit használva): $\begin{array}{c}{\displaystyle \Delta E_{\text{rugalmas}}=\sum _{k=1}^n\frac{D_k}{2}\left[{\left(\Delta {\ell }_k+{\delta }_k\right)}^2-{\left(\Delta {\ell }_k\right)}^2\right]=\sum _{k=1}^n{D}_k\left(\Delta {\ell }_k{\delta }_k+\frac{1}{2}{\left({\delta }_k\right)}^2\right)\mathrm{.}}\end{array}$ Tudjuk, hogy $D_k=\frac{DL}{{\ell }_k}$, $\Delta {\ell }_k=k{\ell }_k$ és ${\delta }_k=\frac{{\ell }_k}{L}\delta$, innen kapjuk, hogy $\begin{array}{c}{\displaystyle \Delta E_{\text{rugalmas}}=D\delta \sum _{k=1}^{n}k{\ell }_k+\frac{1}{2}D{\delta }^2\sum _{k=1}^n\frac{{\ell }_k}{L}\mathrm{.}}\end{array}$ A jobb oldal második tagja éppen $W$-vel egyezik meg, így ‐ a munkatétel egyenlete szerint ‐ a tömegközéppont lesüllyedése ($mg=DL$ és $n=5$ esetén): $\begin{array}{c}{\displaystyle \Delta h=\frac{\delta }{L}\sum _{k=1}^{5}k{\ell }_k=\left(1\cdot \frac{30}{87}+2\cdot \frac{20}{87}+3\cdot \frac{15}{87}+4\cdot \frac{12}{87}+5\cdot \frac{10}{87}\right)\delta =\frac{71}{145}\delta \mathrm{.}}\end{array}$