| Feladat: | B.4607 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Török Zsombor | ||
| Füzet: | 2015/január, 22 - 24. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Feladat, Beírt kör, Síkgeometriai bizonyítások, Háromszög területe | ||
| Hivatkozás(ok): | Feladatok: 2014/február: B.4607 | ||
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.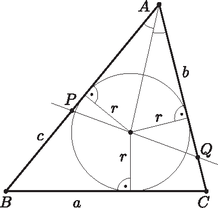 1. ábra Írjuk fel az háromszög területét kétféleképpen:
Legyen a szög nagysága , , és (2. ábra). Ekkor 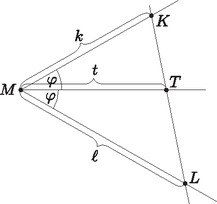 2. ábra Ezután eredeti feladatunk megoldása már egyszerű. Használjuk az I. megoldás jelöléseit, továbbá legyen a -ből induló szögfelező és az oldal metszéspontja . A szögfelezőtétel szerint a és oldalak arányában osztja az szakaszt, ezért . Másrészt rajta van az szögfelezőin, ezért a szögre és az pontra alkalmazhatjuk segédtételünket. E szerint |