Feladat:	B.4602	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kosztolányi Kata ,  Nagy-György Zoltán
Füzet:	2015/január, 19. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Trapézok, Húrnégyszögek
Hivatkozás(ok):	Feladatok: 2014/február: B.4602

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.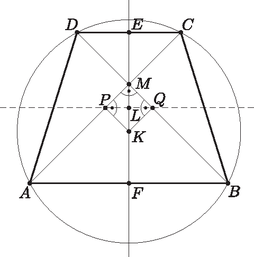   I. megoldás. Az 1. ábra jelöléseit használva, legyenek $E$ és $F$ az alapok felezőpontjai, $P$ és $Q$ az átlók felezőpontjai; $P$ és $Q$ egyenlő távolságra vannak az alapoktól, így rajta vannak a trapéz középvonalán.   1. ábra   A trapéz átlói a körülírt kör húrjai, ezért felező merőlegesük átmegy a kör $K$ középpontján. $PM=QM$, ezért és a derékszögek miatt a $PKQM$ négyszög négyzet. Legyen a $PQ$ szakasz felezőpontja $L$. Mivel $L$ illeszkedik a trapéz középvonalára, $LE=LF$. Az $L$ pont a $PKQM$ négyzet középpontja, így 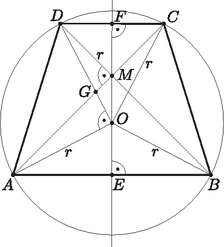$LM=LK$, vagyis $\begin{array}{c}{\displaystyle ME=LE-LM=LF-LK=KF\mathrm{,}}\end{array}$ és ezt kellett bizonyítanunk.   II. megoldás. A 2. ábra jelöléseit használva $AEO\sphericalangle =DFO\sphericalangle ={90}^{\circ }$ és $AOE\sphericalangle ={180}^{\circ }-{90}^{\circ }-DOF\sphericalangle ={90}^{\circ }-DOF\sphericalangle$, ezért az $AEO$ és $OFD$ háromszögek egybevágók (szögeik páronként egyenlők és $AO=OD=r$). Ebből következik, hogy $EO=DF$.   2. ábra   Az átlók derékszöget zárnak be, és $EF$ szimmetria tengely, ezért a $DCM$ derékszögű háromszöget az $FM$ oldalfelező merőleges két egyenlő szárú derékszögű háromszögre bontja. Ebből pedig már következik, hogy $FM=DF=EO$.