Feladat: 2014. évi Nemzetközi Matematika Diákolimpia 23. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Ágoston Péter 
Füzet: 2014/október, 394 - 395. oldal  PDF  |  MathML 
Témakör(ök): Nemzetközi Matematikai Diákolimpia, Síkgeometriai bizonyítások, Teljes indukció módszere, Ponthalmazok
Hivatkozás(ok):Feladatok: 2014/szeptember: 2014. évi Nemzetközi Matematika Diákolimpia 23. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ágoston Péter megoldása. Vegyük úgy, hogy az egyenesek kezdetben feketék, és jelentse egy egyenes pirosra színezése azt, hogy azt az egyenest már nem színezhetjük kékre.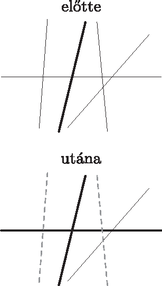
Ekkor teljes indukcióval belátható, hogy minden n-nél nem nagyobb k-ra ki lehet színezni k darab egyenest kékre úgy, hogy legfeljebb k2-k darabot színeztünk pirosra, és minden két szomszédos kék oldallal rendelkező véges tartománynak van piros oldala.
Kezdőlépés: egy egyenest ki lehet így színezni, hiszen ekkor 0 egyenest kell pirosra színeznünk, mivel nyilvánvalóan nincs olyan véges tartomány, amelynek két szomszédos kék oldala lenne.
Indukciós lépés: ha k-1 egyenest már sikerült így kékre színezni, akkor kiszínezhetünk a feketék közül egy tetszőlegesen választott k-adikat is kékre és néhány alkalmasan választottat pirosra úgy, hogy a színezés megfeleljen az indukciós feltételnek. A pirosakat ugyanis elég úgy megválasztani, hogy az újonnan keletkezett szomszédos kék oldalpárú véges tartományoknak legyen ilyen oldala (a többire már biztosítva van), vagyis azoknak, amelyeknek az egyik oldala a szomszédos kékek közül az új kék egyenes. Vegyük fel az új kék egyenesnek a korábbi k-1 kék egyenessel vett metszéspontjaihoz egyik, illetve másik irányban legközelebb levő egyenes metszéspontjait, és amennyiben ezekben nem kék egyenes metszi az új kék egyenest, színezzük ezeket az egyeneseket pirosra (vagy hagyjuk meg annak) (1. ábra).


 

1. ábra
 

Ezzel legfeljebb 2⋅(k-1)=2k-2 egyenest színeztünk pirosra, és ,,szerencsés'' esetben biztosítottuk a feltétel teljesülését az összes olyan véges tartományra, amelynek a két szomszédos kék oldalegyenese között szerepel az új egyenes. Előfordulhat azonban, hogy a legszélső, kék egyenessel vett metszéspont a legszélső metszéspont is egyben, ekkor nincs mit kiszínezni azon az oldalon, de nem is kell, hiszen az ezen az oldalon levő tartományok nyilvánvalóan végtelenek. Az is előfordulhat, hogy két pirosra színezendő egyenes egybeesik (ha csak egy metszéspont van két kék egyenessel vett metszéspont között), de ezzel is csak megspórolunk egy pirosra színezést (2. ábra).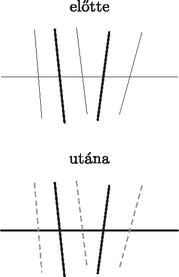


 

2. ábra
 

Ugyanakkor ha két kék egyenessel vett metszéspont szomszédos, akkor nem tudunk köztük semmit sem pirosra színezni, de így megspóroltunk két egyenesszínezést, amit a feltétel teljesítése érdekében még felhasználhatunk. Ennyi elég is, ugyanis ha a szomszédos kék egyenesek között levő, az új kék egyenessel mint oldallal rendelkező tartományok közül valamelyik véges, annak biztosan van piros vagy fekete oldala, hiszen ha csak kék lenne, lett volna eddig is két szomszédos kék oldala, így az indukciós feltétel szerint legalább egy piros is, ami ellentmondás. Ezt az oldalt tehát pirosra lehet színezni (vagy meghagyni annak) (3. ábra). (Az ábrákon a vastag vonal kék egyenest jelöl, a vékony vonal feketét, a szaggatott pedig pirosat.)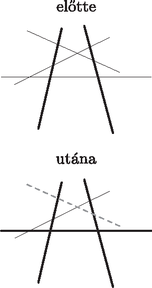


 

3. ábra
 

Tehát legfeljebb két egyenesszínezéssel ekkor is biztosítani lehet a két sokszögre a feltételt, vagyis összességében nem nőtt a pirosra színezett egyenesek száma, azaz továbbra is legfeljebb 2k-2 új piros egyenes keletkezett. Így mivel eddig legfeljebb (k-1)2-(k-1)=k2-2k+1-k+1=k2-3k+2 egyenes volt piros, ezután legfeljebb k2-3k+2+2k-2=k2-k egyenes piros, és az indukciós feltételnek eleget tettünk.
Tehát amíg k nem haladja meg n-et, tudunk olyan színezést, amely összesen legfeljebb k2 egyenest színez ki kékre vagy pirosra, és minden olyan véges tartomány, amelynek van két szomszédos kék oldala, rendelkezik piros oldallal is. Tehát ha kiszíneztünk [n] egyenest kékre így, és [n]≠n, akkor még van fekete egyenes, amelyet így nyugodtan kékre színezhetünk, hiszen a két szomszédos kék oldallal rendelkező véges tartományokból már nem csinálhat teljesen kék kerületű véges tartományt, és nyilvánvalóan a többiből sem. Így viszont kiszíneztünk legalább n egyenest kékre (ha [n]=n, akkor is), és nincs csupa kék véges tartomány, vagyis az állítást beláttuk minden n-re.