Kezdőlap


Feladat:	2014. évi Nemzetközi Matematika Diákolimpia 22. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Di Giovanni Márk
Füzet:	2014/október, 392 - 394. oldal		PDF \| MathML
Témakör(ök):	Nemzetközi Matematikai Diákolimpia, Számsorozatok, Teljes indukció módszere
Hivatkozás(ok):	Feladatok: 2014/szeptember: 2014. évi Nemzetközi Matematika Diákolimpia 22. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Di Giovanni Márk megoldása. Lássuk be a feladat általánosítását, azaz $n - \frac{1}{2}$ összértékű érmékre és $n$ dobozra, teljes indukcióval ( $n = 100$ -ra a feladat állítását kapjuk).
$n = 1$ -re az állítás triviális, mert az összes érmét berakhatjuk egyetlen dobozba.
Tegyük fel most, hogy $m - 1$ -ig igaz az állítás ( $m \geq 2$ ) és lássuk be $m$ -re.
Ha van néhány érme, amelyek összértéke 1, akkor azokat berakhatjuk az első dobozba, ezzel visszavezetve az $m - 1$ -es esetre, amit már beláttunk. Tehát mostantól feltehetjük, hogy nincsenek ilyen érmék.
Továbbá ha van kettő darab $1 / 2 t$ értékű érménk, akkor azokat lecserélhetjük egy darab $1 / t$ értékű érmére, mivel ha így el tudjuk végezni az elhelyezést, akkor az eredeti érméket is el tudjuk helyezni. Tehát feltehetjük, hogy minden páros nevezőjű érméből legfeljebb 1 darab van.
Rakjuk bele a dobozokba az érméket mohó algoritmussal, azaz vesszük a legnagyobb, addig nem elhelyezett érmét és belerakjuk az egyik dobozba (mint majd kiderül, lényegtelen, hogy melyikbe). Ha ezzel az algoritmussal sikerült elhelyezni az összes érmét, akkor készen vagyunk és az állítást beláttuk. Ha nem, akkor elakadtunk egy $\frac{1}{b}$ értékű érménél. Eddig a dobozokban csak olyan érmék szerepelhetnek, amelyek legalább $1 / b$ értékűek (a mohó algoritmus miatt). Továbbá minden dobozban a kimaradt hely kisebb mint $1 / b$ , különben oda be tudnánk rakni még legalább egy kimaradt érmét. Legyen az üres hely mérete az $i$ -edik dobozban $a_{i}$ . Ekkor $\frac{1}{b} > {max}_{}^{} {a_{i}}$ . Továbbá

\begin{matrix} (m - 1) \cdot {max}_{}^{} {a_{i}} \geq \sum a_{i} - {max}_{}^{} {a_{i}} > \sum a_{i} - \frac{1}{b} \geq \frac{1}{2} . \end{matrix}

Az utolsó egyenlőtlenség azért teljesül, mert az összes érme értékösszege legfeljebb

m - \frac{1}{2}

, így a dobozokban lévő érmék értékösszege meg az

1 / b

-s érmének az összege is legfeljebb

m - \frac{1}{2}

.
Ebből adódik:

\begin{matrix} {max}_{}^{} {a_{i}} > \frac{1}{m - 1} \cdot \frac{1}{2}, \end{matrix}

azaz

\frac{1}{b} > \frac{1}{2 m - 2}

, de mivel

b

egész, ezért

\frac{1}{b} \geq \frac{1}{2 m - 3}

.
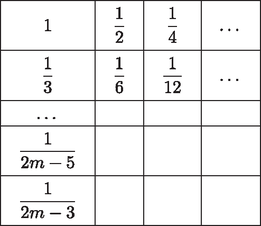
Rakjuk bele az eddigi dobozokban lévő érméket értékeik szerint a következő táblázatba (egy mezőre akár több érme is kerülhet):

Nyilvánvalóan mivel

b \leq 2 m - 3,

ezért a táblázatba kerülő legkisebb elem legalább

\frac{1}{2 m - 3}

értékű.
Most nézzünk meg egy sort: az első mező kivételével minden mező nevezője páros, feltevésünk szerint tehát legfeljebb 1 érme lehet rajta. Vizsgáljuk meg az értékösszeget abban a sorban, ahol az első mező

\frac{1}{2 t - 1}

. A mezők összértéke az első mezőt leszámítva legfeljebb akkora, mint a mezőkön lévő számok összege (hiszen minden mezőn legfeljebb egy érme lehet). Ez az összeg pedig biztosan kisebb, mint annak a végtelen mértani sornak az összege, melynek első néhány eleme szerepel a mezőkön.
Tehát

\begin{matrix} összeg < \sum_{i = 1}^{\infty} \frac{1}{2 t - 1} \cdot \frac{1}{2^{i}} = \frac{1}{2 t - 1} \cdot \sum_{i = 1}^{\infty} \frac{1}{2^{i}} = \frac{1}{2 t - 1} . \end{matrix}

Az első mezőn legfeljebb

2 t - 2

darab érme lehet, különben ki lehetne választani közülük

2 t - 1

darabot, melyek összege 1. Így az értékösszeg a sorban biztosan kisebb, mint

\begin{matrix} (2 t - 2) \cdot \frac{1}{2 t - 1} + \frac{1}{2 t - 1} = 1. \end{matrix}

Mivel ezt a gondolatmenetet elvégezhetjük az összes sorra, ezért minden sorösszeg kisebb, mint 1. Mivel a táblázat

m - 1

darab sorból áll, így a táblázatban lévő érmék összértéke kisebb, mint

m - 1

. Innen

\begin{matrix} \sum a_{i} = m - \sum táblázat > m - (m - 1) = 1. \end{matrix}

Ekkor

{max}_{}^{} {a_{i}} > \frac{1}{m}

, azaz

\frac{1}{b} > \frac{1}{m}

.
Adjuk össze újra az érméket a táblázatos módszerrel, viszont most csak

1 / (m - 1)

-ig tartanak a sorok (vagy

1 / (m - 2)

-ig,

m

paritásától függően.)
Így a táblázatban lévő érmék értékösszege kisebb, mint

\frac{m}{2}

, azaz

\begin{matrix} \sum a_{i} = m - \sum táblázat > m - \frac{m}{2} = m / 2, azaz {max}_{}^{} {a_{i}} > \frac{1}{2}, \end{matrix}

azaz 1/b nagyobb, mint

1 / 2

. Ebből az következik, hogy

b = 1

, azaz egy 1 értékű érménél akadunk el. De korábban már feltettük, hogy semelyik néhány érmének az összege sem 1, így nincsen 1 értékű érménk sem, tehát ellentmondásra jutottunk.
Tehát a pakolással nem tudunk elakadni, azaz működik a módszer, így beláttuk

m

-re is. Ezzel beláttuk az indukciós lépést, így minden

n

-re igaz az állítás, azaz speciális esetként

n = 100

-ra is.