Feladat: 2014. évi Nemzetközi Matematika Diákolimpia 13. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Fehér Zsombor 
Füzet: 2014/október, 389 - 391. oldal  PDF  |  MathML 
Témakör(ök): Nemzetközi Matematikai Diákolimpia, Síkgeometriai bizonyítások, Háromszög nevezetes körei, Háromszög nevezetes vonalai
Hivatkozás(ok):Feladatok: 2014/szeptember: 2014. évi Nemzetközi Matematika Diákolimpia 13. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Fehér Zsombor megoldása. Mindenekelőtt a CHS∢-CSB∢=90∘ feltételt fogjuk értelmezni. Ehhez vegyük fel az AB egyenesen azt az X pontot, melyre SHX∢ derékszög (1. ábra). Ekkor CHX∢=CHS-90∘=CSB∢. Tehát CHX∢=CSX∢, így CHSX húrnégyszög. És mivel SHX∢=90∘, ezért a Thalész-tétel alapján a CHSX kör középpontja SX felezőpontja, ami legyen 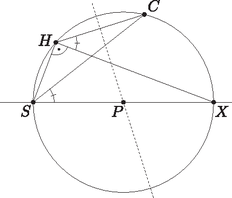P.


 

1. ábra
 

A TSH háromszög körülírt körének középpontját az SH és TH oldalak szakaszfelező merőlegesének metszéspontjaként fogjuk meghatározni (2. ábra). SH felezőmerőlegese ugyanaz, mint SPH∢ szögfelezője, hiszen PSH egyenlőszárú háromszög. Ezáltal az ábra már is sokat egyszerűsödött: csak vesszük HC felezőmerőlegesét, ez P-ben és Q-ban metszi AB-t és AD-t, majd tekintjük a HPA∢ és HQA∢ szögfelezőjét (a belső szögfelezőt, mert az S és a T pont az AP, illetve az AQ szakasz belsejében helyezkedik el). Azt kell belátnunk, hogy ezek metszéspontja rajta van az AH szakaszon, hiszen ekkor AH⊥BD miatt BD valóban érinteni fogja a THS k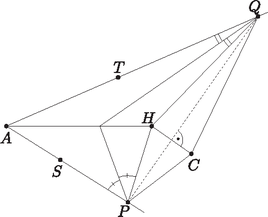ört.


 

2. ábra
 

 
Lemma. Tetszőleges KLMN négyszögre a K-ból és M-ből kiinduló belső szögfelezők pontosan akkor metszik egymást az LN átlón, mint amikor az L-ből és N-ből kiinduló szögfelezők a KM átlón.
 
Bizonyítás. A szögfelezőtétel alapján, ha a K, M szögfelezők mindketten az O pontban metszik LN-t, akkor KL/KN=OL/ON=ML/MN. Így KL/ML=KN/MN alapján az L, N szögfelezők ugyanolyan arányban osztják a KM szakaszt, azaz ugyanott metszik a KM átlót. Vagyis mindkettő pontosan akkor teljesül, ha a négyszög szemközti oldalainak szorzata egyenlő.
A lemmát alkalmazva az APHQ négyszögre, azt kell belátnunk, hogy a PAQ∢ és PHQ∢ szögfelezője a PQ egyenesen metszi egymást.
Még nem használtuk a feladat ABC∢=CDA∢=90∘ feltételét (3. ábra). Ez alapján ABCD húrnégyszög, így 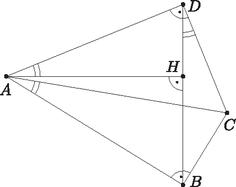BAC∢=BDC∢=90∘-ADH∢=HAD∢.


 

3. ábra
 

 
Megjegyzés. A feladat B és D pontját, illetve az ott lévő derékszögeket tulajdonképpen csak arra használjuk, hogy BAC∢=HAD∢ teljesüljön. Valójában a C pontot szabadon mozgathatjuk az AC egyenesen, az állítás érvényben marad.

Legyen az AHC kör és a PQ egyenes metszéspontja E (4. ábra). Mivel HC felezőmerőlegesén van E, a HC ív felezőpontja E, ezért HAE∢=EAC∢. És mivel QAH∢=CAP∢, a QAP szögfelezője nem más, mint AE. Az AHC kör középpontja rajta van HC felezőmerőlegesén, PQ-n, ezáltal a kör tükrös PQ-ra. Azon pontok halmaza, melyek P-től és Q-tól mért távolságainak aránya állandó, és ez az állandó AP/AQ, egy Apollóniusz-kör. Mégpedig egy olyan Apollóniusz-kör, ami átmegy A-n, és a szögfelezőtétel miatt E-n, emellett tükrös a PQ egyenesre. Így ez a kör csak az AHC kör lehet. Tehát H is rajta van az Apollóniusz-körön, így HP/HQ=AP/AQ, és PHQ∢ szögfelezője is átmegy E-n. Ezzel a feladat állítását bebizonyítottuk.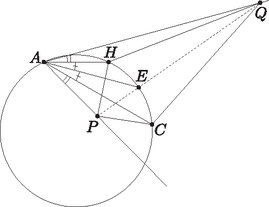


 

4. ábra
 

 
Megjegyzések. 1. Amennyiben az A, H, C pontok egy egyenesre esnek, az Apollóniusz-kör helyét egy felező merőleges veszi fel. Ebben az esetben az egész ábra szimmetrikus, a feladat állítása pedig triviális. Annak ellenére, hogy ráadásul a fenti bizonyítás is lényegében ugyanúgy működik, a versenyzők ezen megjegyzés hiányában ‐ mint minden speciális eset elmulasztásáért ‐ maximálisan 6 pontot kaphattak.
2. A megoldás utolsó lépésének alapja a következő egyszerű, de mégis meglepő tétel, amit érdemes lehet megjegyezni:
 
Tétel. Ha ABCD deltoid, akkor a {P∣APB∢≡DPC∢(mod180∘)} halmaz, vagyis azon pontok mértani helye, melyekből az AB és DC szakaszok ugyanakkora irányított szögben látszanak, egy kör és egy egyenes (rombusz esetén két egyenes). A kör a fent látott Apollóniusz-kör, az egyenes pedig a deltoid szimmetriatengelye.
 
Ezt a tételt alkalmaztuk feladatunkban a PHQC deltoidra: mivel PAC∢=HAQ∢, ezért AP/AQ=HP/HQ, készen vagyunk. Ugyanakkor a tétel használatával pl. Lapunk B. 4448. feladata (2012. április) is könnyen adódik ‐ ezt Olvasónkra bízzuk, hogyan.