Kezdőlap


Feladat:	2015. évi Nemzetközi Fizika Diákolimpia 2. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2015/november, 488 - 491. oldal		PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia, Egyéb feladatok, Young-féle (kétréses) interferencia, Fermat-elv, de Broglie-hipotézis
Hivatkozás(ok):	Feladatok: 2015/október: 2015. évi Nemzetközi Fizika Diákolimpia 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A rész. Szélsőértékelv a mechanikában
A.1. A mechanikai energia megmaradása alapján:

\begin{matrix} \frac{1}{2} m v_{1}^{2} = \frac{1}{2} m v_{2}^{2} + V_{0}, amiből v_{2} = \sqrt[]{v_{1}^{2} - \frac{2 V_{0}}{m}} . \end{matrix}

A.2. A határfelületen csak az

x

irányú sebességkomponens változik (a határfelületen fellépő

- x

irányú erőlökés hatására), az

y

irányú nem. Ezért

\begin{matrix} v_{1 y} & = v_{2 y}, \\ v_{1} sin ϑ_{1} & = v_{2} sin ϑ_{2} . \end{matrix}

A.3. A hatás definíciójának megfelelően

A (w)

O

és

P

rögzített pontok között:

\begin{matrix} A (w) = m v_{1} \sqrt[]{x_{1}^{2} + w^{2}} + m v_{2} \sqrt[]{{(x_{0} - x_{1})}^{2} + (y_{0}^{2} - w^{2})} . \end{matrix}

A (w)

hatás akkor lesz minimális, ha

w

szerinti deriváltja nulla:

\begin{matrix} \frac{v_{1} w}{\sqrt[]{x_{1}^{2} + w^{2}}} - \frac{v_{2} (y_{0} - w)}{\sqrt[]{{x_{0} - x_{1})}^{2} + {(y_{0} - w)}^{2}}} = 0, \\ \frac{v_{1}}{v_{2}} = \frac{(y_{0} - w) \sqrt[]{x_{1}^{2} + w^{2}}}{w \sqrt[]{{(x_{0} - x_{1})}^{2} + {(y_{0} - w)}^{2}}} . \end{matrix}

Vegyük észre, hogy ez ugyanaz, mint az A.2.-ben megkapott

v_{1} sin ϑ_{1} = v_{2} sin ϑ_{2}

eredmény!

B rész. Szélsőértékelv az optikában
B.1. A fény sebessége az I-es közegben

c / n_{1}

, a II-es közegben

c / n_{2}

, ahol

c

a fénysebesség vákuumban. Legyen a két közeget elválasztó egyenes egyenlete

y = y_{0}

, a fénysugár pedig az

x = w

helyen lépjen át egyik közegből a másikba. Az a

τ (w)

idő, amíg a fény a

(0; 0)

origóból a rögzített

(x_{0}; y_{0})

pontba jut:

\begin{matrix} τ (w) = \frac{n_{1}}{c} \sqrt[]{y_{1}^{2} + w^{2}} + \frac{n_{2}}{c} \sqrt[]{{(x_{0} - w)}^{2} + {(y_{0} - y_{1})}^{2}} . \end{matrix}

A szélsőértéket A.3.-hoz hasonlóan deriválással határozhatjuk meg:

\begin{matrix} \frac{n_{1} w}{\sqrt[]{y_{1}^{2} + w^{2}}} - \frac{n_{2} (y_{0} - w)}{\sqrt[]{{(x_{0} - w)}^{2} + {(y_{0} - y_{1})}^{2}}} = 0, \\ n_{1} sin α_{1} = n_{2} sin α_{2} . \end{matrix}

Ez a Snellius‐Descartes-törvény.
B.2. A Snellius‐Descartes-törvény alapján

n_{0} sin α_{0} = n (y) sin α

. Ezen kívül felhasználva, hogy

d y / d x = - ctg α

és

sin α = 1 / \sqrt[]{1 + ctg^{2} α}

\begin{matrix} n_{0} sin α_{0} = \frac{n (y)}{\sqrt[]{1 + {(\frac{d y}{d x})}^{2}}}, \frac{d y}{d x} = - \sqrt[]{{(\frac{n (y)}{n_{0} sin α_{0}})}^{2} - 1} . \end{matrix}

B.3. A B.2. eredményből a változókat szétválasztva és mindkét oldalt integrálva:

\begin{matrix} \int \frac{d y}{\sqrt[]{{(\frac{n_{0} - k y}{n_{0}})}^{2} - 1}} = - \int d x . \end{matrix}

(Felhasználtuk, hogy

α_{0} = 90^{\circ}

és így

sin α_{0} = 1

.) Használjuk a

ξ = (n_{0} - k y) / n_{0}

helyettesítést, így:

\begin{matrix} \int \frac{d ξ (- \frac{n_{0}}{k})}{\sqrt[]{ξ^{2} - 1}} = - \int d x, - \frac{n_{0}}{k} ln (\frac{n_{0} - k y}{n_{0}} + \sqrt[]{{(\frac{n_{0} - k y}{n_{0}})}^{2} - 1}) = - x + c . \end{matrix}

Figyelembe véve az

x = 0

és

y = 0

kezdeti feltételeket

c = 0

. Ebből a pálya egyenlete:

\begin{matrix} x = \frac{n_{0}}{k} ln [(\frac{n_{0} - k y}{n_{0}}) + \sqrt[]{{(\frac{n_{0} - k y}{n_{0}})}^{2} - 1}] . \end{matrix}

B.4. Felhasználva a megadott adatokat (

y_{0} = 10, 0 cm

n_{0} = 1, 50

k = 0, 050 cm^{- 1}

) a B.3. végeredményébe behelyettesítve

(y = - y_{0})

\begin{matrix} x_{0} = \frac{n_{0}}{k} ln [(\frac{n_{0} + k y_{0}}{n_{0}}) + \sqrt[]{{(\frac{n_{0} + k y_{0}}{n_{0}})}^{2} - 1}] = 24, 0 cm . \end{matrix}

C rész. A szélsőértékelv és az anyag hullámtermészete
C.1. A részecske de Broglie-hullámhossza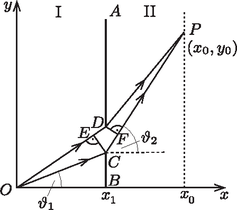

λ = \frac{h}{m v}

, amiből a keresett fáziskülönbség (a hatás

Δ A = m v Δ s

definícióját felhasználva):

\begin{matrix} Δ φ = \frac{2 π}{λ} Δ s = \frac{2 π}{h} m v Δ s = \frac{2 π Δ A}{h} . \end{matrix}

C.2. Tanulmányozzuk az

O C P

és

O D P

pályákat! A geometriai útkülönbség az I-es tartományban

E D

, a II-es tartományban

C F

. Ebből

d ≪ x_{0} - x_{1}

és

d ≪ x_{1}

felhasználásával

\begin{matrix} Δ φ_{C D} & = \frac{2 π d sin ϑ_{1}}{λ_{1}} - \frac{2 π d sin ϑ_{2}}{λ_{2}} = \\ = \frac{2 π m v_{1} d sin ϑ_{1}}{h} - \frac{2 π m v_{2} d sin ϑ_{2}}{h} = \\ = 2 π \frac{m d}{h} (v_{1} sin ϑ_{1} - v_{2} sin ϑ_{2}) = 0 \end{matrix}

(A.2. vagy B.1. alapján). Ez az eredmény várható, hiszen a klasszikus pálya közelében erősítésnek kell lennie.

D rész. Anyaghullámok interferenciája
D.1. Az energiák alapján

\begin{matrix} q U_{1} = \frac{1}{2} m v^{2}, amiből U_{1} = \frac{m v^{2}}{2 q} = 1, 139 \cdot 10^{3} V . \end{matrix}

D.2. A fáziskülönbség

P

-ben:

\begin{matrix} Δ φ_{P} = \frac{2 π d sin ϑ}{λ_{1}} - \frac{2 π d sin ϑ}{λ_{2}} = 2 π (v_{1} - v_{2}) \frac{m d}{h} sin ϑ = 2 π β, \end{matrix}

amiből

\begin{matrix} β = 5, 13. \end{matrix}

D.3. Az előző rész alapján látható, hogy a legközelebbi olyan helyen, ahol nem várható elektronbecsapódás (kioltás van)

Δ φ = 5, 5 \cdot 2 π

. Ez alapján:

\begin{matrix} \frac{m v_{1} d sin ϑ}{h} - \frac{m v_{2} d sin (ϑ + Δ ϑ)}{h} = 5, 5; \\ sin (ϑ + Δ ϑ) = \frac{\frac{m v_{1} d sin ϑ}{h} - 5, 5}{\frac{m v_{2} d}{h}} = \frac{v_{1}}{v_{2}} sin ϑ - \frac{5, 5 h}{m v_{2} d} = 0, 173 586, \\ Δ ϑ = - 0, 0036^{\circ}, \end{matrix}

amiből a

P

-hez legközelebbi hely távolsága:

\begin{matrix} Δ y = (x_{0} - x_{1}) [tg (ϑ + Δ ϑ) - tg ϑ] = - 16, 2 μ m . \end{matrix}

A negatív előjel azt mutatja, hogy ez a pont

P

alatt van.
D.4. Az

I

fluxussűrűség az elektronok

v

sebességének és

N / V

sűrűségének szorzata. Ez alapján:

\begin{matrix} N = \frac{I_{{min}_{}^{}} V}{v} = 1, amiből I_{{min}_{}^{}} = \frac{v}{V} = \frac{v}{A l} = 4 \cdot 10^{19} m^{- 2} s^{- 1} . \end{matrix}