Kezdőlap


Feladat:	2015. évi Nemzetközi Fizika Diákolimpia 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2015/november, 485 - 488. oldal		PDF \| MathML
Témakör(ök):	Magfúzió, Nemzetközi Fizika Diákolimpia, A Nap energiatermelése, Neutrínó
Hivatkozás(ok):	Feladatok: 2015/október: 2015. évi Nemzetközi Fizika Diákolimpia 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A rész. A Naptól jövő sugárzás
A.1. A Stefan‐Boltzmann-törvény alapján: $L_{⊙} = (4 π R_{⊙}^{2}) (σ T_{⊙}^{4})$ . Innen:

\begin{matrix} T_{⊙} = {(\frac{L_{⊙}}{4 π R_{⊙}^{2} σ})}^{1 / 4} = 5, 76 \cdot 10^{3} K . \end{matrix}

A.2.

\begin{matrix} P_{be} = \int_{0}^{\infty} u (f) d f = \int_{0}^{\infty} A \frac{R_{⊙}^{2}}{d_{⊙}^{2}} \frac{2 π h}{c^{2}} f^{3} exp (- h f / k_{B} T_{⊙}) d f . \end{matrix}

Legyen

x = \frac{h f}{k_{B} T_{⊙}}

. Ekkor

f = \frac{k_{B} T_{⊙}}{h} x

és

d f = \frac{k_{B} T_{⊙}}{h} d x

. Ezzel:

\begin{matrix} P_{be} = \frac{2 π h A R_{⊙}^{2}}{c^{2} d_{⊙}^{2}} \frac{{(k_{B} T_{⊙})}^{4}}{h^{4}} \int_{0}^{\infty} x^{3} e^{- x} d x = \frac{2 π k_{B}^{4}}{c^{2} h^{3}} T_{⊙}^{4} A \frac{R_{⊙}^{2}}{d_{⊙}^{2}} \cdot 6 = \frac{12 π k_{B}^{4}}{c^{2} h^{3}} T_{⊙}^{4} A \frac{R_{⊙}^{2}}{d_{⊙}^{2}} . \end{matrix}

Másik megoldás, amely nem használja a Wien-közelítést:

\begin{matrix} P_{be} = \frac{L_{⊙}}{4 π d_{⊙}^{2}} A = σ T_{⊙}^{4} A \frac{R_{⊙}^{2}}{d_{⊙}^{2}} = \frac{2 π^{5} k_{B}^{4}}{15 c^{2} h^{3}} T_{⊙}^{4} A \frac{R_{⊙}^{2}}{d_{⊙}^{2}} . \end{matrix}

A.3.

\begin{matrix} n_{γ} (f) = \frac{u (f)}{h f} = A \frac{R_{⊙}^{2}}{d_{⊙}^{2}} \frac{2 π}{c^{2}} f^{2} exp (- h f / k_{B} T_{⊙}) . \end{matrix}

A.4. A hasznos kimenő teljesítményt az

E_{g} = h f_{g}

egy fotonra jutó energiakvantum és az

E \geq E_{g}

energiájú fotonok számának szorzata adja:

\begin{matrix} P_{ki} & = h f_{g} \int_{f_{g}}^{\infty} n_{γ} (f) d f = h f_{g} A \frac{R_{⊙}^{2}}{d_{⊙}^{2}} \frac{2 π}{c^{2}} \int_{f_{g}}^{\infty} f^{2} exp (- h f / k_{B} T_{⊙}) d f = \\ = k_{B} T_{⊙} x_{g} A \frac{R_{⊙}^{2}}{d_{⊙}^{2}} \frac{2 π}{c^{2}} {(\frac{k_{B} T_{⊙}}{h})}^{3} \int_{x_{g}}^{\infty} x^{2} e^{- x} d x = \\ = \frac{2 π k_{B}^{4}}{c^{2} h^{3}} T_{⊙}^{4} A \frac{R_{⊙}^{2}}{d_{⊙}^{2}} x_{g} (x_{g}^{2} + 2 x_{g} + 2) e^{- x_{g}} . \end{matrix}

A.5. A hatásfok:

\begin{matrix} η = \frac{P_{ki}}{P_{be}} = \frac{x_{g}}{6} (x_{g}^{2} + 2 x_{g} + 2) e^{- x_{g}} . \end{matrix}

P_{be}

-re az A.2. másik eredményét használjuk, akkor a hatásfok:

\begin{matrix} η = \frac{2 π k_{B}^{4}}{c^{2} h^{3}} \frac{1}{σ} x_{g} (x_{g}^{2} + 2 x_{g} + 2) e^{- x_{g}} = (\frac{90}{π^{4}}) \frac{x_{g}}{6} (x_{g}^{2} + 2 x_{g} + 2) e^{- x_{g}} . \end{matrix}

A két eredmény közel van egymáshoz, mert 90/

π^{4} \approx 0, 92 \approx 1

.
A.6.

\begin{matrix} η = \frac{1}{6} (x_{g}^{3} + 2 x_{g}^{2} + 2 x_{g}) e^{- x_{g}} . \end{matrix}

A határokon érvényes értékek:

η (0) = 0

és

η (\infty) = 0

.
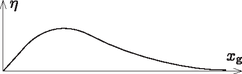
Mivel a zárójelben levő polinom kizárólag pozitív együtthatókat tartalmaz, az monoton növekvő. Az exponenciális függvény monoton csökkenő, és a szorzatuknak valahol maximuma van.

\begin{matrix} \frac{d η}{d x_{g}} = \frac{1}{6} (- x_{g}^{3} + x_{g}^{2} + 2 x_{g} + 2) e^{- x_{g}}, \\ {\frac{d η}{d x_{g}} |}_{x_{g} = 0} = \frac{1}{3}, {\frac{d η}{d x_{g}} |}_{x_{g} \to \infty} = 0. \end{matrix}

Ha az A.2. másik eredményét használjuk, akkor:

\begin{matrix} \frac{d η}{d x_{g}} = \frac{15}{π^{4}} (- x_{g}^{3} + x_{g}^{2} + 2 x_{g} + 2) e^{- x_{g}}, \\ {\frac{d η}{d x_{g}} |}_{x_{g} = 0} = \frac{30}{π^{4}} \approx 0, 31, {\frac{d η}{d x_{g}} |}_{x_{g} \to \infty} = 0. \end{matrix}

A.7. A maximális értéket ott veszi fel a függvény, ahol

\begin{matrix} \frac{d η}{d x_{g}} = \frac{1}{6} (- x_{g}^{3} + x_{g}^{2} + 2 x_{g} + 2) e^{- x_{g}} = 0 \Rightarrow p (x_{g}) \equiv x_{g}^{3} - x_{g}^{2} - 2 x_{g} - 2 = 0. \end{matrix}

Az egyenlet megoldásához használhatjuk például a felező módszert (más numerikus módszer is elfogadható):

\begin{matrix} p (0) & = - 2, \\ p (1) & = - 4, \\ p (2) & = - 2, \\ p (3) & = 10 \Rightarrow 2 < x_{0} < 3, \\ p (2, 5) & = 2, 375 \Rightarrow 2 < x_{0} < 2, 5, \\ p (2, 25) & = - 0, 171 \Rightarrow 2, 25 < x_{0} < 2, 5. \end{matrix}

A közelítő érték, ahol

η

-nak maximuma van:

x_{0} = 2, 27

. A maximum:

η (2, 27) = 0, 457

.
A.8. Az

x_{g}

értéke:

\begin{matrix} x_{g} = \frac{1, 11 \cdot 1, 60 \cdot 10^{- 19}}{1, 38 \cdot 10^{- 23} \cdot 5763} = 2, 23, \end{matrix}

amivel a hatásfok:

\begin{matrix} η_{Si} = \frac{x_{g}}{6} (x_{g}^{2} + 2 x_{g} + 2) e^{- x_{g}} = 0, 457. \end{matrix}

Ha az A.2. másik eredményét használjuk, akkor:

\begin{matrix} η_{Si} = \frac{15 x_{g}}{π^{4}} (x_{g}^{2} + 2 x_{g} + 2) e^{- x_{g}} = 0, 422. \end{matrix}

A.9. A Nap teljes gravitációs potenciális energiája:

\begin{matrix} Ω = - \int_{0}^{M_{⊙}} \frac{G m d m}{r} . \end{matrix}

Az egyenletes tömegeloszlás miatt:

\begin{matrix} ϱ = \frac{3 M_{⊙}}{4 π R_{⊙}^{3}}, m = \frac{4}{3} π r^{3} ϱ, d m = 4 π r^{2} ϱ d r . \end{matrix}

Ezzel:

\begin{matrix} Ω = - \int_{0}^{R_{⊙}} G (\frac{4}{3} π r^{3} ϱ) (4 π r^{2} ϱ) \frac{d r}{r} = - \frac{16 π^{2} G ϱ^{2}}{3} \frac{R_{⊙}^{5}}{5} = - \frac{3}{5} \frac{G M_{⊙}^{2}}{R_{⊙}} . \end{matrix}

A.10.

\begin{matrix} τ_{KH} = \frac{- Ω}{L_{⊙}} = \frac{3 G M_{⊙}^{2}}{5 R_{⊙} L_{⊙}} = 1, 88 \cdot 10^{7} év . \end{matrix}

B rész. A Napból jövő neutrínók
B.1.

Δ E

energia felszabadulása során két neutrínó keletkezik, így

\begin{matrix} Φ_{ν} = 2 \cdot \frac{L_{⊙}}{4 π d_{⊙}^{2} Δ E} = 2 \cdot \frac{3, 85 \cdot 10^{26}}{4 π \cdot {(1, 50 \cdot 10^{11})}^{2} \cdot 4, 0 \cdot 10^{- 12}} = 6, 8 \cdot 10^{14} m^{- 2} s^{- 2} . \end{matrix}

B.2. Legyen

ε

a neutrínó detektálásának hatásfoka,

N_{0}

a bejövő részecskeszám. Ezzel:

\begin{matrix} N_{1} & = ε N_{0}, \\ N_{e} & = ε N_{0} (1 - r), \\ N_{x} & = ε N_{0} r / 6, \\ N_{2} & = N_{e} + N_{x} . \end{matrix}

Tehát:

\begin{matrix} (1 - r) N_{1} + \frac{r}{6} N_{1} = N_{2}, \end{matrix}

innen a kérdezett hányados:

\begin{matrix} r = \frac{6}{5} (1 - \frac{N_{2}}{N_{1}}) . \end{matrix}

B.3. Amikor egy elektron már éppen nem bocsát ki Cserenkov-sugárzást, a sebessége

v_{stop} = c / n

-re csökken. Az elektron teljes energiája ekkor:

\begin{matrix} E_{stop} = \frac{m_{e} c^{2}}{\sqrt[]{1 - v_{stop}^{2} / c^{2}}} = \frac{n m_{e} c^{2}}{\sqrt[]{n^{2} - 1}} . \end{matrix}

Abban a pillanatban, miután a neutrínó kiütötte az elektront, az elektron energiája:

\begin{matrix} E_{start} = α Δ t + \frac{n m_{e} c^{2}}{\sqrt[]{n^{2} - 1}} . \end{matrix}

A kölcsönhatás előtt az elektron energiája

m_{e} c^{2}

. Így a neutrínónak átadott energia:

\begin{matrix} E_{átadott} = E_{start} - m_{e} c^{2} = α Δ t + (\frac{n}{\sqrt[]{n^{2} - 1}} - 1) m_{e} c^{2} . \end{matrix}

B.4. A

^{7}

Be atommagok mozgása miatt Doppler-effektus lép fel a neutrínókra. Mivel az energia relatív megváltozása kicsiny (

Δ E_{rms} / E_{ν} \sim 10^{- 4}

), a nemrelativisztikus Doppler-eltolódással lehet számolni (a relativisztikus számolás szinte azonos eredményt ad). A megfigyelés irányának a

z

irányt véve:

\begin{matrix} \frac{Δ E_{rms}}{E_{ν}} = \frac{v_{z, rms}}{c} = \frac{\frac{1}{\sqrt[]{3}} V_{Be}}{c} = 3, 85 \cdot 10^{- 4} . \end{matrix}

Tehát a Be atommagok sebességének négyzetes középértéke:

\begin{matrix} V_{Be} = \sqrt[]{3} \cdot 3, 85 \cdot 10^{- 4} \cdot 3, 00 \cdot 10^{8} {ms}^{- 1} = 2, 01 \cdot 10^{5} {ms}^{- 1} . \end{matrix}

A Nap magjának átlagos hőmérséklete pedig:

\begin{matrix} \frac{1}{2} m_{Be} V_{Be}^{2} = \frac{3}{2} k_{B} T_{c} \Rightarrow T_{c} = 1, 13 \cdot 10^{7} K . \end{matrix}