Feladat:	B.4579	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Baran Zsuzsanna ,  Di Giovanni Márk ,  Dinev Georgi ,  Fonyó Viktória ,  Katona Dániel ,  Kocsis Júlia ,  Kovács Balázs Marcell ,  Lajkó Kálmán ,  Leipold Péter ,  Leitereg Miklós ,  Maga Balázs ,  Nagy-György Pál ,  Nemes György ,  Simkó Irén ,  Vágó Ákos ,  Varga Péter ,  Vető Bálint ,  Viharos Lóránd Ottó ,  Williams Kada
Füzet:	2014/december, 527 - 530. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Polinomok szorzattá alakítása, Algebrai átalakítások, Kör egyenlete
Hivatkozás(ok):	Feladatok: 2013/november: B.4579

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Tegyük fel, hogy a polinom szorzattá alakítható, $\begin{array}{c}{\displaystyle x\left(x+4\right)+a\left(y^2-1\right)+2by=\left(Ax+By+C\right)\left(Dx+Ey+F\right)\mathrm{,}}\end{array}$ ahol $A$, $B$, $C$, $D$, $E$ és $F$ valós számok. Mivel két polinom pontosan akkor egyezik meg, ha megfelelő együtthatóik megegyeznek, és az eredeti polinomban $x^2$ együtthatója 1, azért $AD=1$. Az első lineáris tényezőt $A$-val, a másodikat pedig $D$-vel osztva szintén az eredeti polinom két elsőfokú polinom szorzatára való felbontását kapjuk, ezért elegendő az $\begin{array}{c}{\displaystyle x\left(x+4\right)+a\left(y^2-1\right)+2by=\left(x+uy+v\right)\left(x+py+q\right)}\end{array}$ alakú szorzatra bonthatóság feltételét megadnunk. A megfelelő együtthatókat összehasonlítva a következő egyenleteket kapjuk: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle y^2:}& {\displaystyle a=up\mathrm{,}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle xy:}& {\displaystyle 0=u+p\mathrm{,}}\hfill & \text{(<mn>2</mn>)}\\ \hfill {\displaystyle x:}& {\displaystyle 4=v+q\mathrm{,}}\hfill & \text{(<mn>3</mn>)}\\ \hfill {\displaystyle y:}& {\displaystyle 2b=uq+vp\mathrm{,}}\hfill & \text{(<mn>4</mn>)}\\ \hfill {\displaystyle \text{konstans: }}& {\displaystyle -a=vq\mathrm{.}}\hfill & \text{(<mn>5</mn>)}\end{array}}$ Ha $a=0$, akkor (1) és (2) miatt $u=p=0$, s így (4)-ből adódik, hogy csak $b=0$ esetén lehetséges a szorzattá bontás (ebben az esetben viszont az eredeti polinom nem kétváltozós). Ha $a\ne 0$, akkor (1) miatt $u\ne 0$. A (2) egyenletből $p=-u$, amit (1)-be, illetve (4)-be írva kapjuk, hogy $a=-u^2$ és $2b=u\left(q-v\right)$. Ez utóbbiból $q-v=2b/u$ következik, s így (3)-at figyelembe véve $q=2+b/u$ és $v=2-b/u$. Végül ezeket (5)-be beírva $\begin{array}{c}{\displaystyle -a=\left(2-\frac{b}{u}\right)\left(2+\frac{b}{u}\right)=4-\frac{b^2}{u^2}=4-\frac{b^2}{-a}\mathrm{,}}\end{array}$ azaz $a^2=-4a-b^2$, vagyis ${\left(a+2\right)}^2+b^2=4$. 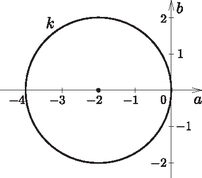Ez a $\left(-\mathrm{2,0}\right)$ középpontú, 2 sugarú $k$ kör egyenlete. Tehát ha a polinom szorzattá bontható, akkor az $\left(a;b\right)$ pont rajta van $k$-n. Megfordítva, ha $k$ egy tetszőleges $\left(c;d\right)$ pontját vesszük, akkor $c\le 0$ teljesül. Ha $c=0$, akkor $d=0$ is teljesül. A $\left(0;0\right)$ párhoz a nyilvánvalóan szorzattá bomló $x\left(x+4\right)$ polinom tartozik. Ha $c\ne 0$, akkor legyen $\begin{array}{c}{\displaystyle u=\sqrt[]{-c}\mathrm{,}p=-\sqrt[]{-c}\mathrm{,}v=2-\frac{d}{\sqrt[]{-c}}\text{és}q=2+\frac{d}{\sqrt[]{-c}}\mathrm{.}}\end{array}$     Egyszerű számolással adódik, hogy $\begin{array}{c}{\displaystyle \left(x+uy+v\right)\left(x+py+q\right)=x^2+4x+c{y}^2+2dy-c\mathrm{,}}\end{array}$ vagyis az eredeti polinom két elsőfokú polinom szorzatára bomlik. Tehát a keresett mértani hely a $\left(-2;0\right)$ középpontú, 2 sugarú kör.   II. megoldás. Koordinátageometriai módszerekkel kicsit kevesebb számolással is belátható az I. megoldásban megadott feltétel szükségessége. A következő gondolatmenettel viszont a feltétel elégségességét nem tudjuk belátni. Alkalmazzuk az $x=w-2$, $y=z+1$ lineáris helyettesítést. Ekkor $\begin{array}{c}{\displaystyle P\left(x\mathrm{,}y\right)=x\left(x+4\right)+a\left(y^2-1\right)+2by=w^2+a{z}^2+2\left(a+b\right)z+2b-4=Q\left(w\mathrm{,}z\right)\mathrm{.}}\end{array}$ Mivel lineáris helyettesítésnél elsőfokú polinomból elsőfokú polinomot kapunk, $P\left(x\mathrm{,}y\right)$ pontosan akkor bomlik két elsőfokú polinom szorzatára, amikor $Q\left(w\mathrm{,}z\right)$ felbomlik. Tekintsük a $Q\left(w\mathrm{,}z\right)=0$ egyenletnek eleget tevő pontokat a síkon. Ha $\begin{array}{c}{\displaystyle Q\left(w\mathrm{,}z\right)=\left(Aw+Bz+C\right)\left(Dw+Ez+F\right)\mathrm{,}}\end{array}$ akkor ezek a pontok az $\begin{array}{c}{\displaystyle Aw+Bz+C=0\text{és}Dw+Ez+F=0}\end{array}$ egyenletű (esetleg egybeeső) egyeneseket alkotják. Mivel $Q\left(w\mathrm{,}z\right)$-ben $w^2$ együtthatója 1, ezért a felbontásban szereplő együtthatókra $AD=1$ teljesül, tehát az egyenesek egyike sem párhuzamos a $w$ koordinátatengellyel. Ha $a=0$ és $b\ne 0$, akkor $\begin{array}{c}{\displaystyle z=-\frac{1}{2b}{w}^2-1+\frac{2}{b}\mathrm{,}}\end{array}$ ami egy parabola egyenlete, tehát ebben az esetben nem bontható fel a polinom lineáris tényezőkre. Ha viszont $a=b=0$, akkor $Q\left(w\mathrm{,}z\right)=w^2$, ami nyilván felbontható például $w\cdot w$ alakban. Ekkor a tényezőknek megfelelő két egyenes egybeesik. Ha $a\ne 0$, akkor $Q\left(w\mathrm{,}z\right)$-ben szerepel $z^2$-es tag, ezért mindkét lineáris tényezőnek kell tartalmaznia $cz$ típusú tagot ahol $c\ne 0$ egy valós szám. Ez azt jelenti, hogy a tényezőknek megfelelő egyenesek egyike sem párhuzamos az $z$ koordinátatengellyel, azaz minden $d$ valós szám esetén a $z=d$ egyenletű egyenes metszi a $Q\left(w\mathrm{,}z\right)=0$ egyenletű ponthalmazt. A $Q\left(w\mathrm{,}z\right)=0$ egyenletet átrendezve kapjuk, hogy $\begin{array}{c}{\displaystyle w^2=-a{z}^2-2\left(a+b\right)z-2b+4.}\end{array}$ Mivel $w^2\ge 0$, ezért a bal oldalon lévő ($a\ne 0$ miatt) másodfokú polinom egyetlen $z=d$ helyettesítésre sem vehet fel negatív értéket, mert az azt jelentené, hogy a $z=d$ egyenletű egyenes nem metszené a $Q\left(w\mathrm{,}z\right)=0$ egyenletű ponthalmazt. Másrészt viszont a $w=0$ egyenletű egyenes nem párhuzamos a ponthalmazt alkotó egyenesekkel, ezért metszi a ponthalmazt, vagyis a $\begin{array}{c}{\displaystyle -a{z}^2-2\left(a+b\right)z-2b+4=0}\end{array}$ (6) egyenletnek van gyöke. E két feltétel pontosan akkor teljesül egyszerre, ha a (6) egyenlet diszkriminánsa 0. Tehát $a\ne 0$ esetén ha $Q\left(w\mathrm{,}z\right)$ lineáris tényezőkre bomlik, akkor $\begin{array}{c}{\displaystyle {\left(-2\left(a+b\right)\right)}^2-4\left(-a\right)\left(-2b+4\right)=\mathrm{0,}\text{azaz}{\left(a+2\right)}^2+b^2=4.}\end{array}$   Megjegyzés. A második megoldásból is megkapható a feltétel elégségessége, ehhez azonban a másodfokú egyenletekkel adott ponthalmazok az ún. másodrendű görbék alaposabb ismerete szükséges. Írjuk a $P\left(x\mathrm{,}y\right)$ polinomot mátrix alakba a következőképpen: $\begin{array}{c}{\displaystyle \left(x+4\right)+a\left(y^2-1\right)+2by=\left(x\mathrm{,}y\mathrm{,1}\right)M{\left(x\mathrm{,}y\mathrm{,1}\right)}^T\mathrm{,}}\end{array}$ ahol Ismert tétel, hogy a polinom akkor és csak akkor alakítható szorzattá a komplex számok körében, ha $\text{det}M=0$. A tényezőkben szereplő együtthatók akkor valósak, ha az is teljesül, hogy az $M$ mátrix bal felső $2\times 2$-es részmátrixának determinánsa nempozitív.