Feladat:	4696. fizika feladat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Fekete Panna ,  Németh Flóra Boróka
Füzet:	2015/szeptember, 376 - 378. oldal		PDF  |  MathML
Témakör(ök):	Egyéb feladatok, Feladat, Egyéb merev testek mechanikája
Hivatkozás(ok):	Feladatok: 2015/január: 4696. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Jelöljük a gyógyszertabletták alapkörének sugarát $r$-rel, magasságukat pedig $m$-mel! Az asztalra függőleges $\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}$ sebességgel leeső tabletta annak megfelelően kerül gurulós, vagy nem gurulós helyzetbe, hogy a tabletta milyen irányban helyezkedik el a $\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}$ vektorhoz képest, vagy ami ugyanezt jelenti: a $\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}$ vektor milyen irányba mutat a tablettához viszonyítva. Ezeket az irányokat jellemezhetjük például azzal, hogy a $\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}$ vektor (vagy annak meghosszabbítása) melyik pontban döfi át a tabletta köré rajzolt $R=\sqrt[]{r^2+{\left(m/2\right)}^2}$ sugarú gömbfelületet. Ha a döféspont az 1. ábra bal felén látható módon a gömbfelület vastagon jelölt gömbövébe esik, akkor a tabletta (ha nem pattan fel) a hengerpalástjára, tehát gurulós helyzetbe kerül. Ha viszont a döféspont a szaggatott vonallal jelölt két gömbsüveg valamelyik pontja (lásd az 1. ábra jobb felét), akkor a tabletta valamelyik körlapján áll meg, tehát nem tud elgurulni az asztalon. 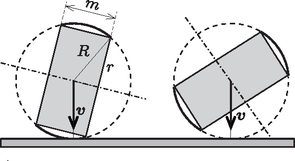  1. ábra   A gurulós helyzetbe kerülő gyógyszertabletták számának és az összes lehulló tabletta számának aránya (sok leeső tabletta esetén) a gurulós helyzet valószínűségével egyezik meg. Véges sok kimenetellel rendelkező eseményeknél (például a kockadobásoknál) a valószínűséget a kedvező esetek számának és az összes lehetséges eset számának hányadosaként kaphatjuk meg. (A ,,kedvező'' esemény a valószínűségszámítás szokásos szóhasználata, jóllehet esetünkben a gyógyszer elgurulása inkább kedvezőtlennek tekintendő.) Bonyolultabb a helyzet akkor, ha az események lehetséges végkimenetelének száma és a ,,kedvező'' események lehetséges száma is (elvben) végtelen. Ilyenkor a valószínűséget ‐ nyilván ‐ nem számolhatjuk ki két ,,végtelen nagy szám'' hányadosaként. Az ún. folytonos valószínűségeloszlások kezelésének egyik, esetenként jól használható módja a geometriai módszer.1 Ha az események kimenetele egy felület pontjaival (esetünkben a gömbfelület egy-egy pontjával) jellemezhető, akkor a kérdéses esemény valószínűsége a kedvező eseményeknek megfelelő felületdarab felszínének és az összes lehetséges eseményhez tartozó teljes felület felszínének hányadosaként számítható ki. Jelen esetben ez a valószínűség $\begin{array}{c}{\displaystyle P_{\text{elgurul}}=\frac{A_{\text{gömböv}}}{A_{\text{gömbfelszín}}}=\frac{2mR\pi }{4R^2\pi }=\frac{m}{2\sqrt[]{r^2+{\left(m/2\right)}^2}}=\frac{1}{\sqrt[]{5}}\approx 0\mathrm{,}45.}\end{array}$ A lehulló gyógyszertablettáknak tehát ‐ várhatóan ‐ mintegy 45 százaléka fog elgurulni.   Megjegyzések. 1. A valószínűség geometriai módszerrel történő kiszámítása nem egyértelmű, és emiatt kellő körültekintést igényel. Ha például a gyógyszertabletta köré nem gömböt, hanem ‐ mondjuk ‐ egy nagyobb kockát képzelünk, a leeső tabletta térbeli helyzetét a középpontján átmenő függőleges egyenes és a kocka felszínének döféspontjával is jellemezhetjük. A keresett valószínűség azonban nem egyezik meg a kocka felszínén mért megfelelő területek arányával; ha mégis így számolunk, hibás eredményt kapunk. Azt, hogy mit jelent a ,,minden térbeli irány egyenlő valószínűségű'' kifejezés (vagyis hogy milyen felületen mért területek aránya adja meg helyesen a valószínűséget) fizikai feltételek szabják meg. A legtermészetesebb gondolatunkat, miszerint az irányok valószínűségeloszlása a gömbfelületen vett ,,mérték'' szerint egyenletes, kellően pörgő, bukdácsolva leeső tablettáknál a tapasztalat is megerősíti. Lehetne azonban olyan ,,tablettaejtő gépet'' konstruálni, amely használatával más valószínűségeloszlás alakulhatna ki. A mechanikusan kevert golyókkal történő lottósorsolásnál a szkeptikusok régi dilemmája: vajon elég alapos-e a keverés, egyforma-e az esélye (a húzási valószínűsége) mindegyik számnak? 2. Sok versenyző úgy érvelt, hogy mivel az egész feladat (a tabletta leesése és a feltett kérdés is) a henger alakú gyógyszertabletta forgástengelyére nézve szimmetrikus, a probléma 2 dimenziós feladatként kezelhető. Ha ez így helyes lenne, a kérdéses valószínűség az 1. ábrán látható vastagon jelölt körívek hosszának és a teljes kör hosszának arányával (a megadott számadatok mellett kb. 0,3-mal) egyezne meg. Az érvelés azonban hibás, egy 3 dimenziós probléma néha még akkor sem kezelhető síkbeli feladatként, ha az elrendezés és a kérdésfeltevés bizonyos tengely körüli (valamekkora szögű) elforgatásokra nézve szimmetrikus. Jól látható ez egy hatlapú dobókockánál. Ha azt kérdezzük, mekkora valószínűséggel esik a (jól megpörgetett) kocka két szemközti (a 2. ábrán sötétebben jelölt) lapjának valamelyikére, a helyes válasz nyilván $1/3$, hiszen a kocka köré rajzolt gömb felületének éppen egyharmadát fedik le a ,,kedvező'' esetnek megfelelő pontok. Ha viszont a kockát oldalnézetben rajzoljuk le (2. ábra jobb oldala), és a feladatot (a másik 4 lap szimmetrikus helyzete miatt) 2 dimenziósnak terkintjük, a keresett valószínűségre (a körívek hosszából) a hibás 1/2 ,,eredményt'' kapjuk. 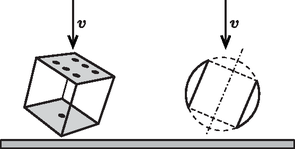  2. ábra   1Lásd pl. ezt a cikket a KöMaL honlapján: http://www.komal.hu/cikkek/valszam/valszam.h.shtml.