Feladat:	2012. évi Eötvös fizikaverseny 2. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Radnai Gyula
Füzet:	2013/március, 169 - 171. oldal		PDF  |  MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén), Vastag lencse
Hivatkozás(ok):	Feladatok: 2013/március: 2012. évi Eötvös fizikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.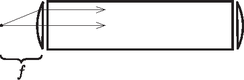   Megoldás. $a)$ Ha azt szeretnénk, hogy a rúd másik végétől ugyanakkora távolságra találkozzanak az onnan kilépő fénysugarak, akkor egy nyilvánvaló megoldás erre az, hogy a rúd egyik külső fókuszába helyezzük el a pontszerű fényforrást. Az ebből kiinduló fénysugarak a rúd belsejében párhuzamosan haladnak, majd a másik végénél kilépve újra fókusztávolságnyira egyesülnek. Tovább egyszerűsíti a megoldást, ha gondolatban levágjuk a rúd végeit. Ezáltal két vékony lencsét és közöttük egy ,,plánparalel'' réteget kapunk (3. ábra). 3. ábra   A vékony, síkdomború lencse fókusztávolságára $\begin{array}{c}{\displaystyle \frac{1}{f}=\left(n-1\right)\left(\frac{1}{R_1}+\frac{1}{R_2}\right)\mathrm{,}\text{most}{R}_2\to \infty \mathrm{.}}\end{array}$ Így $\begin{array}{c}{\displaystyle f=\frac{R}{n-1}=\frac{1\text{cm}}{1\mathrm{,}5-1}=2\text{cm}\mathrm{.}}\end{array}$ Van azonban egy másik lehetséges megoldás is! Ekkor a fénysugarak nem párhuzamosan haladnak a rúd belsejében, hanem a rúd közepén találkoznak, majd ebből a pontból kiindulva érik el a rúd másik végét. Ott kilépve éppen olyan messze találkoznak, mint amilyen távolságra voltak a rúd első végétől, amikor elindultak. Ez is egy szimmetrikus sugármenet, de most már nem segít a megoldásban az előbbi ,,felszeletelés''. Vizsgáljuk meg általánosan az első felület adta leképezést! Legyen a kiindulási $T$ tárgypont a rúdvégtől $t$ távolságra, keletkezzék ennek $K$ képe a rúd belsejében $k$ távolságra a leképező rúdvégtől. További jelölések a 4. ábrán láthatók. 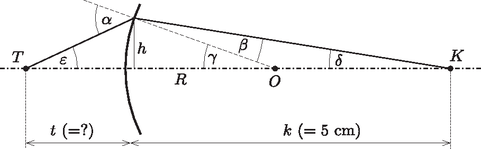4. ábra   Az ábráról leolvasható, hogy $\alpha =\epsilon +\gamma$, valamint $\gamma =\beta +\delta$. Mindegyik szög külön-külön is kicsi, ezért a Snellius‐Descartes-törvény felhasználásával $\begin{array}{c}{\displaystyle n=\frac{\text{sin}\alpha }{\text{sin}\beta }\approx \frac{\alpha }{\beta }=\frac{\epsilon +\gamma }{\gamma -\delta }\mathrm{.}}\end{array}$ Ebből ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle n\left(\gamma -\delta \right)}& {\displaystyle =\epsilon +\gamma \mathrm{,}}\hfill \\ \hfill {\displaystyle n\gamma -\gamma }& {\displaystyle =\epsilon +n\delta \mathrm{,}}\hfill \\ \hfill {\displaystyle \left(n-1\right)\frac{h}{R}}& {\displaystyle =\frac{h}{t}+n\frac{h}{k}\mathrm{,}}\hfill \end{array}}}\hfill \\ \hfill {\displaystyle \frac{1}{t}+\frac{n}{k}=\left(n-1\right)\frac{1}{R}\Rightarrow \frac{1}{t}+\frac{1\mathrm{,}5}{5\text{cm}}=\frac{0\mathrm{,}5}{1\text{cm}}\Rightarrow t=5\text{cm. }}\hfill \end{array}}$ A kétféle sugármenet tehát a következő: 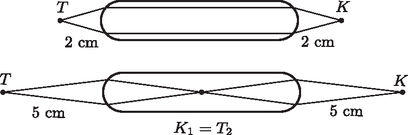5. ábra   $b)$ Tekintsük a 6. ábrát! 6. ábra   Az előző gondolatmenethez hasonlóan most is meghatározhatnánk a kis szöget bezáró fénysugarakra érvényes leképezési törvényeket. Helykímélés céljából ezt itt nem tesszük meg, de bárki ellenőrizheti, hogy a két végnél a következőket kapjuk: $\begin{array}{c}{\displaystyle \frac{1}{t_1}+\frac{n}{k_1}=\frac{n-1}{R}\mathrm{,}\text{illetve}\frac{n}{t_2}+\frac{1}{k_2}=\frac{n-1}{R}\mathrm{.}}\end{array}$ (Megjegyezni úgy lehet, hogy mindig azt a kép-, illetve tárgytávolságot kell osztani $n$-nel, amelyik az üvegben van.) A keresett $t_1$ távolságot $x$-szel jelölve: $\begin{array}{c}{\displaystyle \frac{1}{x}+\frac{1\mathrm{,}5}{k_1}=\frac{0\mathrm{,}5}{1\text{cm}}\mathrm{,}\text{illetve}\frac{1\mathrm{,}5}{10\text{cm}-k_1}+\frac{1}{2x}=\frac{0\mathrm{,}5}{1\text{cm}}\mathrm{.}}\end{array}$ Ebből $x$-re másodfokú egyenlet adódik, megoldása: $\begin{array}{c}{\displaystyle x_1=4\text{cm};x_2=1\mathrm{,}25\text{cm}\mathrm{.}}\end{array}$ Ellenőrzésképpen kiszámíthatjuk az új képpontok helyzetét. Eredményünket a 7. ábra mutatja. 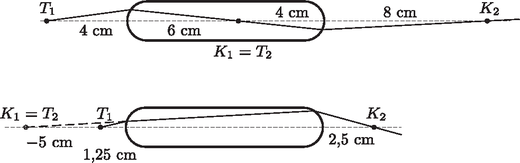7. ábra. $x=4$ cm esetén $k_1=6$ cm, $t_2=4$ cm, $k_2=8$ cm. $x=1\mathrm{,}25$ cm esetén $k_1=-5$ cm, $t_2=15$ cm, $k_2=2\mathrm{,}5$ cm   Megjegyzések. 1. További megoldásokat is kaphatnánk, ha nemcsak a második rúdvégen átmenő, hanem az innen visszaverődő fénysugarakat is vizsgálnánk. Ezek egy része az első felületről is visszaverődik, és újra a második felület felé halad. Itt egy részük kilép, másik részük visszaverődik. Vagyis páros számú visszaverődés után újabb és újabb, egyre halványabb képpontok keletkeznek a rúd másik végéről történő kilépés után a levegőben. Ennek vizsgálatát természetesen nem várta el a versenybizottság. 2. Több versenyző próbálkozott olyan megoldással, amikor az üveghenger oldala is részt vesz a leképezésben. Ez hibás gondolat, mivel a rúd tengelyén lévő pontból kiinduló és a tengellyel kis szöget bezáró fénysugarak az üvegben is a tengely közelében haladnak, nem érhetik el a henger oldalát.