Kezdőlap


Feladat:	2013. évi Nemzetközi Fizika Diákolimpia 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2013/november, 489 - 493. oldal		PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia, Maghasadás, Olvadás, fagyás, Térbeli mozgás
Hivatkozás(ok):	Feladatok: 2013/október: 2013. évi Nemzetközi Fizika Diákolimpia 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. A Maribo-meteorit

A Maribo sebessége
1.1. A meteorit útját az 1. ábra mutatja. A

C

pont az észlelő biztonsági kamera helye,

M

a becsapódási pont,

F

a 155. képkockán,

G

pedig a 161. képkockán észlelt pozíció,

D

és

E

ezeknek a pontoknak a Föld felszínére vett vetülete. A

C B

egyenes észak‐déli irányban áll, az északi irányt a nyíl jelzi.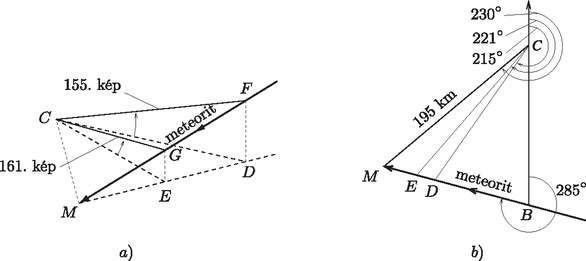

1. ábra. A meteorit pályája a légkörben.

a)

Elforgatott, távlati nézet (nem méretarányos).

b)

Vízszintes síkra vett vetület

A megadott szögeket az

1. b)

vetületi rajzon ívek jelölik. Ezekből megkapható az ábrán az összes többi szög is, és az

| M C | = 195 km

oldal ismeretében, elemi geometriai úton (a szinusz-tétel alkalmazásával) megkaphatóak a következő oldalak:

\begin{matrix} | C D | = 170, 0 km, |CE| = 177,7 km, |DE| =19,77km. \end{matrix}

1. a)

távlati rajzon az ívvel jelölt, ismert magassági szögek segítségével az

F

és

G

pont magassága megkapható:

\begin{matrix} | D F | = | C D | \cdot tg (19, 2^{\circ}) = 59, 20 km, |EG| = |CE|\cdottg(14,7^{\circ}) =46,62 km. \end{matrix}

Ezután a 155. és a 161. képkocka között megtett

| F G |

út Pitagorasz tételéből adódik:

\begin{matrix} | F G | = \sqrt[]{{| D E |}^{2} + {(| D F | - | E G |)}^{2}} = 23, 43 km, \end{matrix}

így a képkockák idejének ismeretében a keresett sebesség:

\begin{matrix} v = \frac{| F G |}{2, 28 s -1,46 s} = 28, 6 \frac{km}{s} . \end{matrix}

Megolvad-e a meteorit az atmoszférában?
1.2a. A légkörben lassuló meteoroidra sebességtől függő, változó erő hat, így mozgását az

\begin{matrix} m_{M} \frac{d v}{d t} = - λ v^{2}, λ = k ϱ_{atm} π R_{M}^{2} \end{matrix}

differenciálegyenlet írja le, mely a változók szétválasztásának módszerével egzaktul megoldható:

\begin{matrix} \frac{d v}{v^{2}} = - \frac{λ}{m_{M}} d t, \int_{v_{M}}^{0, 9 v_{M}} \frac{d v}{v^{2}} = - \int_{0}^{t_{1}} \frac{λ}{m_{M}} d t, - (\frac{1}{0, 9} - 1) \frac{1}{v_{M}} = - \frac{λ}{m_{M}} t_{1} . \end{matrix}

Így a keresett idő:

\begin{matrix} t_{1} = \frac{m_{M}}{k ϱ_{atm} π R_{M}^{2}} (\frac{1}{0, 9} - 1) \frac{1}{v_{M}} = 0, 88 s . \end{matrix}

Differenciálegyenlet nélkül is adható egy igen jó közelítő megoldás. Miközben a sebesség

v_{M}

-ről

0, 9 v_{M}

-re csökken, a közegellenállási erő nem nagyon változik, átlagos értékét vehetjük

F_{átl} = - λ {(0, 95 v_{M})}^{2}

-nek. Ebből a mozgás átlagos lassulása

a_{átl} = \frac{F_{átl}}{m_{M}}

, ahonnan a keresett idő:

\begin{matrix} t_{1} = \frac{- 0, 1 v_{M}}{a_{átl}} = \frac{m_{M}}{k ϱ_{atm} π R_{M}^{2}} \frac{0, 1}{{(0, 95)}^{2}} \frac{1}{v_{M}} = 0, 87 s . \end{matrix}

1.2b. A meteoroid kinetikus energiájának és a teljes megolvasztáshoz szükséges energiának a hányadosa ismert összefüggések alapján:

\begin{matrix} \frac{E_{kin}}{E_{olv}} = \frac{\frac{1}{2} m_{M} v_{M}^{2}}{c_{kő} m_{kő} (T_{kő} - T_{0}) + m_{kő} L_{kő}} = 2, 1 \cdot 10^{2} ≫ 1. \end{matrix}

A Maribo melegedése a légkörön való áthatolás alatt
1.3a. Az

x \approx t^{α} ϱ_{kő}^{β} c_{kő}^{γ} k_{kő}^{δ}

összefüggésben csak a dimenziókat megtartva az

\begin{matrix} 1 m = {(1 s)}^{α} \cdot {(1 \frac{kg}{m^{3}})}^{β} \cdot {(1 \frac{m^{2}}{s^{2} K})}^{γ} \cdot {(1 \frac{kg  m}{s^{3} K})}^{δ} \end{matrix}

egyenletet kapjuk, ami a keresett kitevőkre a

\begin{matrix} β + δ = 0, - 3 β + 2 γ + δ = 1, α - 2 γ - 3 δ = 0, - γ - δ = 0 \end{matrix}

lineáris egyenletrendszert adja. Ennek megoldása

\begin{matrix} α = δ = \frac{1}{2}, β = γ = - \frac{1}{2}, tehát x \approx \sqrt[]{\frac{k_{kő} t}{ϱ_{kő} c_{kő}}} . \end{matrix}

1.3b. A kapott képletbe beírva az adatokat,

\begin{matrix} x (5 s) = 1, 6 mm és \frac{x}{R_{M}} = \frac{1, 6 mm}{130 mm} = 0, 012. \end{matrix}

A meteorit kora
1.4a. Mivel a

_{37}^{87} Rb

izotóp

_{38}^{87} Sr

-ra való bomlásakor a tömegszám nem változik, a rendszám eggyel nő, negatív béta-bomlásról van szó, melynek egyenlete:

\begin{matrix} _{37}^{87} Rb \to_{38}^{87} Sr + e^{-} + {\bar{ν}}_{e} . \end{matrix}

1.4b. A

^{87} Rb

izotópok száma a bomlás miatt exponenciálisan csökken az idő függvényében, ugyanakkor a

^{87} Sr

izotópok száma az elbomlott

^{87} Rb

izotópok számával nő, tehát:

\begin{matrix} N_{87 Rb} (t) & = N_{87 Rb} (0) e^{- λ t}, \\ N_{87 Sr} (t) & = N_{87 Sr} (0) + (N_{87 Rb} (0) - N_{87 Rb} (t)) = N_{87 Sr} (0) + (e^{λ t} - 1) N_{87 Rb} (t) . \end{matrix}

A második egyenletet elosztva a

^{86} Sr

izotópok számával, megkapjuk az egyidejűségi egyenes egyenletét

\begin{matrix} \frac{N_{87 Sr} (t)}{N_{86 Sr}} = \frac{N_{87 Sr} (0)}{N_{86 Sr}} + (e^{λ t} - 1) \frac{N_{87 Rb} (t)}{N_{86 Sr}}, \end{matrix}

melynek meredeksége valóban

e^{λ t} - 1

.
1.4c.

A grafikonról leolvasható, hogy a meredekség

a = e^{λ t} - 1 = \frac{0, 712 - 0, 700}{0, 25} = 0, 050

. A felezési idő és a bomlási állandó

kapcsolata:

T_{1 / 2} = \frac{ln 2}{λ} = 4, 9 \cdot 10^{10}

év. Így a meteorit életkora:

\begin{matrix} τ_{M} = \frac{ln (1 + a)}{λ} = \frac{ln (1 + a)}{ln 2} T_{1 / 2} = 3, 4 \cdot 10^{9} év . \end{matrix}

Az Encke-üstökös, ahonnan a Maribo-meteorit származhat
A Nap körül keringő Encke-üstökös Naptól mért legkisebb és legnagyobb távolsága:

\begin{matrix} a_{min} = 4, 95 \cdot 10^{10} m és a_{max} = 6, 16 \cdot 10^{11} m . \end{matrix}

1.5. Az Encke üstökös pályájának fél nagytengelye

a_{Encke} = \frac{1}{2} (a_{min} + a_{max}) = 3, 33 \cdot 10^{11} m

. Kepler III. törvényét alkalmazva a Földre és az Encke üstökösre azt kapjuk, hogy:

\begin{matrix} \frac{a_{Encke}^{3}}{t_{Encke}^{2}} = \frac{a_{N-F}^{3}}{t_{Föld}^{2}}, tehát t_{Encke} = \sqrt[]{\frac{a_{Encke}^{3}}{a_{N-F}^{3}}} \cdot t_{Föld} = 3, 30 év = 1, 04 \cdot 10^{8} s . \end{matrix}

Aszteroida-becsapódás hatása a Földre
1.6a. A Föld tehetetlenségi nyomatékát (a forgástengely irányában) elhanyagolhatóan befolyásolja az aszteroida becsapódása, hiszen a becsapódás helye a forgástengelyre esik. Tehát a Föld impulzusmomentumának és a forgástengelyének iránya az ütközés előtt és után is egybeesik. Ezért a forgástengely szögeltérülése helyett a Föld impulzusmomentum-vektorának maximális szögeltérülését határozzuk meg az impulzusmomentum megmaradását felhasználva.
A Föld saját impulzusmomentuma a megadott adatok alapján ismert:

\begin{matrix} N_{F} = Θ_{F} ω_{F} = 0, 83 \frac{2}{5} m_{F} R_{F}^{2} \frac{2 π}{24 h} = 5, 87 \cdot 10^{33} \frac{kg m^{2}}{s} . \end{matrix}

Az Északi sarkra becsapódó aszteroidának a Föld középpontjára vonatkoztatott impulzusmomentuma akkor maximális, ha az aszteroida a Föld forgástengelyére merőlegesen mozog, tehát a felszínre érintőlegesen csapódik be. Ekkor az aszteroida impulzusmomentuma:

N_{aszt} = m_{aszt} v_{aszt} R_{F} = 2, 51 \cdot 10^{26} \frac{{kg m}^{2}}{s}

.
Ütközéskor a Föld impulzusmomentuma az aszteroida impulzusmomentumával változik, ezért a Föld impulzusmomentum-vektorának szögeltérülése akkor a legnagyobb, ha az aszteroida impulzusmomentuma merőleges a Földére. Érintőleges becsapódáskor ez a feltétel is teljesül. Így az impulzusmomentum (és egyben a forgástengely) maximális szögeltérülése:

\begin{matrix} Δ φ \approx tg (Δ ϕ) = \frac{N_{aszt}}{N_{F}} = 4, 27 \cdot 10^{- 8} rad . \end{matrix}

Megjegyezzük, hogy a forgástengelynek a Föld felszínével való metszéspontja

R_{F} Δ φ = 27 cm

-rel mozdul el. Azt is érdemes látni, hogy ez az elmozdulás merőleges az aszteroida becsapódási sebességére, hiszen az aszteroida impulzusmomentumának irányába esik.
1.6b. Az Egyenlítőre való függőleges becsapódáskor nem változik a Föld impulzusmomentuma, hiszen az aszteroida impulzusmomentuma a Föld középpontjára vonatkoztatva zérus. Azonban

Δ Θ_{F} = m_{aszt} R_{F}^{2}

-tel megnő a Föld tehetetlenségi nyomatéka, és ez okozza a szögsebesség lassulását:

\begin{matrix} Θ_{F} ω_{F} = (Θ_{F} + Δ Θ_{F}) (ω_{F} + Δ ω_{F}), Δ ω_{F} & \approx - \frac{Δ Θ_{F} ω_{F}}{Θ_{F}} = - 5, 76 \cdot 10^{- 14} \frac{1}{s} . \end{matrix}

Így a Föld forgási periódusának növekedése:

\begin{matrix} Δ T_{F} = 2 π (\frac{1}{ω_{F} + Δ ω_{F}} - \frac{1}{ω_{F}}) \approx - 2 π \frac{Δ ω_{F}}{ω_{F}^{2}} = 6, 84 \cdot 10^{- 5} s . \end{matrix}

1.6c. Ebben az esetben az aszteroida és a Föld impulzusmomentuma egy egyenesbe esik, és becsapódáskor a Föld impulzusmomentuma és tehetetlenségi nyomatéka is megváltozik. A teljes rendszer impulzusmomentuma megmarad, tehát

\begin{matrix} N_{F} \pm N_{aszt} = (Θ_{F} + Δ Θ_{F}) (ω_{F} + Δ ω_{F}), \\ Δ ω_{F} \approx \frac{- Δ Θ_{F} ω_{F} \pm N_{aszt}}{Θ_{F}} \approx \pm \frac{N_{aszt}}{Θ_{F}} = \pm 3, 11 \cdot 10^{- 12} \frac{1}{s} . \end{matrix}

(Felhasználtuk, hogy

\frac{Δ Θ_{F} ω_{F}}{N_{aszt}} \approx 5 \cdot 10^{- 16} ≪ 1

. A

\pm

előjel azt veszi számításba, hogy az aszteroida impulzusmomentuma azonos vagy ellentétes irányú a Földével.) Innen a Föld forgási periódusának megváltozása:

\begin{matrix} Δ T_{F} \approx - 2 π \frac{Δ ω_{F}}{ω_{F}^{2}} = \mp 3, 62 \cdot 10^{- 3} s . \end{matrix}

Maximális becsapódási sebesség
1.7. A maximális becsapódási sebességet három lépésben határozzuk meg.
Az energiamegmaradás törvénye szerint a Nap gravitációs terében a Naptól a Föld pályasugarával megegyező távolságban az

m

tömegű test maximális

v_{1}

sebességére

\begin{matrix} 0 = \frac{1}{2} m v_{1}^{2} - G \frac{m m_{N}}{a_{N-F}} teljesül,  ahonnan v_{1} = \sqrt[]{\frac{2 G m_{N}}{a_{N-F}}} = 42, 1 \frac{km}{s} . \end{matrix}

Szerencsés esetben a test éppen szembe halad

a pályáján

v_{F} = \frac{2 π a_{N-F}}{1 év} = 29, 8 \frac{km}{s}

sebességgel keringő Földdel, tehát a Föld vonatkoztatási rendszerében a sebessége

v_{1} + v_{F}

.
Most a Föld vonatkoztatási rendszerében írhatjuk föl az energiamegmaradás törvényét:

\begin{matrix} \frac{1}{2} m {(v_{1} + v_{F})}^{2} = \frac{1}{2} m {(v_{becs}^{max})}^{2} - G \frac{m m_{F}}{R_{F}} . \end{matrix}

(A Nap hatását elhanyagolhatjuk, hiszen a Föld közelében a Nap gravitációs potenciálja közel állandó.) Innen a becsapódás maximális sebessége:

\begin{matrix} v_{becs}^{max} = \sqrt[]{{(v_{1} + v_{F})}^{2} + \frac{2 G m_{F}}{R_{F}}} = 72, 8 \frac{km}{s} . \end{matrix}