Feladat:	B.4608	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Öreg Botond
Füzet:	2014/szeptember, 350 - 351. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Vektorok lineáris kombinációi, Súlypont
Hivatkozás(ok):	Feladatok: 2014/február: B.4608

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Jelölje a háromszög területét $T$, az $A$ csúcsból induló magasságát $m_a$, a $BC$ oldal felezőpontja pedig legyen $F$. Nagyítsuk az $\overrightarrow{S{A}_1}$ vektort $F$-ből háromszorosára. Mivel a súlypont harmadolja a súlyvonalat, ezért $S$ képe $A$ lesz, a merőlegesség miatt pedig $A_1$ képe az $ABC$ háromszög $A$ csúcsából induló magasságának a talppontja (1. ábra). Vagyis $3|\overrightarrow{S{A}_1}|=m_a$. Ezért a $2T=a{m}_a$ képletet felhasználva kapjuk, hogy 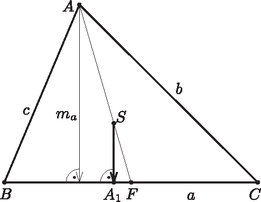$\begin{array}{c}{\displaystyle a^2\overrightarrow{S{A}_1}=a\frac{2T}{3|\overrightarrow{S{A}_1}|}\overrightarrow{S{A}_1}=\frac{2T}{3}a\frac{\overrightarrow{S{A}_1}}{|\overrightarrow{S{A}_1}|}\mathrm{.}}\end{array}$ Ugyanezeket az átalakításokat a másik két tagra is elvégezve a bizonyítandó állítás $\begin{array}{c}{\displaystyle \frac{2T}{3}\left(a\frac{\overrightarrow{S{A}_1}}{|\overrightarrow{S{A}_1}|}+b\frac{\overrightarrow{S{B}_1}}{|\overrightarrow{S{B}_1}|}+c\frac{\overrightarrow{S{C}_1}}{|\overrightarrow{S{C}_1}|}\right)=\text{0}\mathrm{.}}\end{array}$ (1)   1. ábra   Az $a\frac{\overrightarrow{S{A}_1}}{|\overrightarrow{S{A}_1}|}$ vektor hossza $a$, vagyis megegyezik a háromszög $BC$ oldalának hosszával, iránya pedig a $\overrightarrow{BC}$ vektor $-{90}^{\circ }$-os elforgatottja, és hasonló igaz a zárójelben szereplő másik két vektorra is (2. ábra). Ezért ‐ egy tetszőleges $\text{<span style="font-weight: bold;">v</span>}$ vektor $-{90}^{\circ }$-os elforgatottját $\text{<span style="font-weight: bold;">v</span>}\text{'}$-vel jelölve ‐ 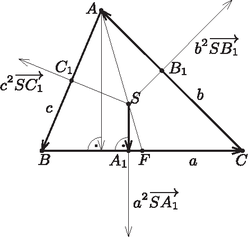$\begin{array}{c}{\displaystyle a\frac{\overrightarrow{S{A}_1}}{|\overrightarrow{S{A}_1}|}+b\frac{\overrightarrow{S{B}_1}}{|\overrightarrow{S{B}_1}|}+c\frac{\overrightarrow{S{C}_1}}{|\overrightarrow{S{C}_1}|}=\overrightarrow{BC}\text{'}+\overrightarrow{CA}\text{'}+\overrightarrow{AB}\text{'}\mathrm{.}}\end{array}$ Vektorok adott szögű elforgatottjainak összege megegyezik az összegük adott szögű elforgatottjával, ezért $\begin{array}{c}{\displaystyle \overrightarrow{BC}\text{'}+\overrightarrow{CA}\text{'}+\overrightarrow{AB}\text{'}=(\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{AB}{)}^{\text{'}}=\text{0}\text{'}=\text{0}\mathrm{,}}\end{array}$ vagyis az (1) egyenlőség teljesül.   2. ábra   Ezzel a feladat állítását igazoltuk.