Feladat:	B.4435	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Czakó Dániel
Füzet:	2014/szeptember, 339 - 340. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Húrnégyszögek, Háromszögek egybevágósága
Hivatkozás(ok):	Feladatok: 2012/március: B.4435

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Azt fogjuk bebizonyítani, hogy $T$ és $F$ rajta van a $KL$ szakasz Thalész-körén. Az $ALCT$ négyszög húrnégyszög, mivel két szemközti szöge derékszög. Az $L$ négyzet középpontja, tehát az $ALC$ háromszög egyenlő szárú derékszögű háromszög, $LCA\sphericalangle ={45}^{\circ }$. A kerületi szögek tétele szerint az $ATL\sphericalangle$ is ${45}^{\circ }$. Ugyanez igaz az $AKTB$ négyszögre is, így az előbbi gondolatmenet szerint kapjuk, hogy $ATK\sphericalangle ={45}^{\circ }$. Ezzel beláttuk, hogy az $LTK\sphericalangle$ derékszög. 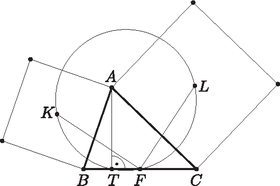    A továbbiakban azt kell bizonyítanunk, hogy $LFK\sphericalangle ={90}^{\circ }$. Ehhez vektorokat használunk. Az $A$ pontból $C$-be mutató vektor legyen $\text{<span style="font-weight: bold;">c</span>}$ és $B$-be mutató vektor legyen $\text{<span style="font-weight: bold;">b</span>}$. Az óramutató járásával ellentétes ${90}^{\circ }$-os elforgatást jelentse a $\text{<span style="font-weight: bold;">v</span>}\text{'}$ jelzés. Az $A$-ból $F$ pontba mutató vektor $\text{<span style="font-weight: bold;">f</span>}=\frac{\text{<span style="font-weight: bold;">b</span>}+\text{<span style="font-weight: bold;">c</span>}}{2}$, az $A$-ból $L$ pontba mutató vektor $\frac{\text{<span style="font-weight: bold;">c</span>}+\text{<span style="font-weight: bold;">c</span>}\text{'}}{2}$, az $A$ pontból $K$-ba mutató pedig $\frac{\text{<span style="font-weight: bold;">b</span>}-\text{<span style="font-weight: bold;">b</span>}\text{'}}{2}$. Ezek segítségével felírható az $\overrightarrow{LF}$ és $\overrightarrow{KF}$ vektor: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \overrightarrow{LF}}& {\displaystyle =\overrightarrow{AF}-\overrightarrow{AL}=\frac{\text{<span style="font-weight: bold;">b</span>}+\text{<span style="font-weight: bold;">c</span>}-\text{<span style="font-weight: bold;">c</span>}-\text{<span style="font-weight: bold;">c</span>}\text{'}}{2}=\frac{\text{<span style="font-weight: bold;">b</span>}-\text{<span style="font-weight: bold;">c</span>}\text{'}}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle \overrightarrow{KF}}& {\displaystyle =\overrightarrow{AF}-\overrightarrow{AK}=\frac{\text{<span style="font-weight: bold;">b</span>}+\text{<span style="font-weight: bold;">c</span>}-\text{<span style="font-weight: bold;">b</span>}+\text{<span style="font-weight: bold;">b</span>}\text{'}}{2}=\frac{\text{<span style="font-weight: bold;">c</span>}+\text{<span style="font-weight: bold;">b</span>}\text{'}}{2}\mathrm{.}}\hfill \end{array}}$ Forgassuk el az $\overrightarrow{LF}$ vektort pozitív irányba ${90}^{\circ }$-kal és használjuk fel, hogy két ${90}^{\circ }$-os elforgatás egymásutánja ${180}^{\circ }$-os elforgatás, tehát a vektorokat ellentettjükre változtatja: $\begin{array}{c}{\displaystyle \overrightarrow{LF}\text{'}=\frac{\left(\text{<span style="font-weight: bold;">b</span>}-\text{<span style="font-weight: bold;">c</span>}\text{'}\right)\text{'}}{2}=\frac{\text{<span style="font-weight: bold;">b'</span>}-\text{<span style="font-weight: bold;">c</span>}\text{'}\text{'}}{2}=\frac{\text{<span style="font-weight: bold;">c</span>}+\text{<span style="font-weight: bold;">b</span>}\text{'}}{2}\mathrm{.}}\end{array}$ Pontosan a $\overrightarrow{KF}$ vektort kaptuk. Ezzel bizonyítottuk, hogy $KTF\sphericalangle =KFL\sphericalangle ={90}^{\circ }$, tehát a $KTFL$ négyszög valóban húrnégyszög.   Megjegyzés: Ha $AB=AC$, akkor $F$ és $T$ egybeesik, az állítás nyilvánvaló.