Feladat:	B.4411	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Ágoston Péter ,  Ágoston Tamás ,  Havasi Márton ,  Janzer Olivér ,  Kiss Melinda Flóra ,  Mester Márton ,  Nagy Róbert ,  Strenner Péter
Füzet:	2014/szeptember, 337 - 339. oldal		PDF  |  MathML
Témakör(ök):	Egyenes körkúpok, Feladat, Térgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 2011/december: B.4411

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Kúpon azt a ponthalmazt értjük, amelynek alkotói teljes egyenesek, azaz a kúp a csúcsától kiindulva mindkét irányban végtelen. Ha ilyen kúpokra belátjuk feladatunk állítását, akkor az a ,,szokásos'' véges kúpokra is teljesül, hiszen minden véges kúp kiterjeszthető végtelen kúppá. Először meghatározzuk a térbeli derékszögű koordinátarendszerben egy olyan egyenes körkúpnak az egyenletét, amelynek tengelye a $z$ tengely, csúcsa az origó, alkotói pedig a $z$-tengellyel $\alpha$ szöget zárnak be. Ekkor a kúpnak a $Z=t$ síkkal vett metszete egy olyan körvonal, amelynek sugara $r=|t|\cdot \text{tg}\alpha$ (1. ábra). Ebben a síkban a körvonal egyenlete $X^2+Y^2=r^2=t^2\cdot \text{tg}{}^2\alpha$, a kúp ezen körvonalak uniója, egyenlete tehát $X^2+Y^2=\text{tg}{}^2\alpha Z^2$. A koordinátarendszer elmozgatására vonatkozó transzformációs képletek alapján ebből az is következik, hogy ha egy olyan kúpnak az egyenletét írjuk fel, amelynek tengelye a $z$ tengely, csúcsa pedig az $\left(u;v;w\right)$ pont, akkor a kúp egyenlete 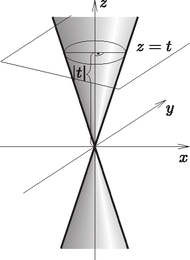$\begin{array}{c}{\displaystyle {\left(X-u\right)}^2+{\left(Y-v\right)}^2=\text{tg}{}^2\alpha {\left(Z-w\right)}^2}\end{array}$ alakú lesz.   1. ábra   Visszatérve feladatunkra vegyünk fel egy derékszögű koordinátarendszert úgy, hogy a $z$ tengely legyen párhuzamos a kúpok tengelyeivel és az első kúp csúcsa legyen az origó. Ha a második kúp csúcsának koordinátái $\left(a;b;c\right)$, a kúpok alkotóinak a tengellyel bezárt szögei pedig $\alpha$ és $\beta$, akkor a kúpok egyenletei $\begin{array}{c}{\displaystyle X^2+Y^2-A{Z}^2=0\text{és}{\left(X-a\right)}^2+{\left(Y-b\right)}^2-B{\left(Z-c\right)}^2=\mathrm{0,}}\end{array}$ (1) ahol $A=\text{tg}{}^2\alpha$ és $B=\text{tg}{}^2\beta$, s mivel a kúpok nyílásszöge különböző, ezekről tudjuk, hogy $0\ne A\ne B\ne 0$. A két kúp közös pontjainak koordinátái mindkét egyenletet kielégítik, sőt kielégítik azok tetszőleges lineáris kombinációját is (vagyis azokat az egyenleteket is, amelyeket úgy kapunk, hogy a két egyenletet tetszőleges számokkal megszorozzuk, majd az így kapott egyenleteket összeadjuk). Szorozzuk be az első egyenletet egy $\lambda$, a másodikat pedig egy $\mu$ számmal úgy, hogy utána összeadva az egyenleteket $X^2$, $Y^2$ és $Z^2$ együtthatója egyaránt 1 legyen. Ehhez a $\lambda +\mu =-A\lambda -B\mu =1$ feltételeket kell kielégíteni, ami a $\begin{array}{c}{\displaystyle \lambda =\frac{B+1}{B-A}\text{és}\mu =-\frac{A+1}{B-A}}\end{array}$ választással elérhető. A két körkúp metszéspontjainak koordinátái tehát kielégítik az így kapott $\begin{array}{c}{\displaystyle \left(X^2-2\mu aX+\mu a^2\right)+\left(Y^2-2\mu bY+\mu b^2\right)+\left(Z^2+2\mu BcZ-\mu B{c}^2\right)=0}\end{array}$ egyenletet. Ezt az egyenletet átalakítva kapjuk, hogy ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left(X-\mu a\right)}^2+{\left(Y-\mu b\right)}^2+{\left(Z+\mu Bc\right)}^2=}\hfill & \text{(<mn>2</mn>)}\\ \hfill {\displaystyle =\left({\mu }^2-\mu \right)a^2+\left({\mu }^2-\mu \right)b^2+\left({\mu }^2{B}^2+\mu B\right)c^2\mathrm{.}}\hfill \end{array}}$ Egyszerű számolással kapjuk, hogy 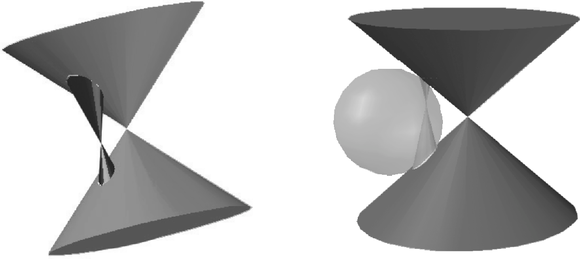${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\mu }^2-\mu }& {\displaystyle =\frac{{\left(A+1\right)}^2+\left(A+1\right)\left(B-A\right)}{{\left(B-A\right)}^2}=\frac{\left(A+1\right)\left(B+1\right)}{{\left(B-A\right)}^2}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{\left(\text{tg}{}^2\alpha +1\right)\left(\text{tg}{}^2\beta +1\right)}{{\left(B-A\right)}^2}>0}\hfill \end{array}}$ és $\begin{array}{c}{\displaystyle {\mu }^2{B}^2+\mu B=\frac{{\left(A+1\right)}^2{B}^2-\left(A+1\right)B\left(B-A\right)}{{\left(B-A\right)}^2}=\frac{AB\left(A+1\right)\left(B+1\right)}{{\left(B-A\right)}^2}>\mathrm{0,}}\end{array}$ tehát a (2) egyenlet jobb oldalán $\left(a;b;c\right)=\left(0;0;0\right)$ esetén $0$, ha pedig $\left(a;b;c\right)\ne \left(0;0;0\right)$, akkor pozitív szám áll. Ezért ez az egyenlet egy (esetleg elfajuló) gömb egyenlete.     2. ábra   Tehát két párhuzamos tengelyű, különböző nyílásszögű egyenes körkúp közös pontjai mindig illeszkednek egy gömbfelületre. Ha a két kúp csúcspontja egybeesik, akkor egyetlen közös pontjuk van (de persze bármely egypontú halmaz is tekinthető egy alkalmas gömb részhalmazának).   Megjegyzés. Ha a két kúp nyílásszöge megegyezik, de a kúpok nem esnek egybe, akkor közös pontjaik egy síkon helyezkednek el. Ebben az esetben ugyanis az (1) egyenletekben mindhárom négyzetes tag együtthatója megegyezik. Ha a két egyenletet kivonjuk egymásból, akkor $\left(a;b;c\right)\ne \left(0;0;0\right)$ miatt egy olyan lineáris egyenletet kapunk, melyben az $X$, $Y$ és $Z$ változók közül legalább az egyik szerepel. Viszont a lineáris egyenletek síkot határoznak meg, tehát a közös pontok ebben az esetben egy síkon vannak.