Kezdőlap


Feladat:	4701. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Kasza Bence , Sal Kristóf , Öreg Botond
Füzet:	2015/május, 309 - 313. oldal		PDF \| MathML
Témakör(ök):	Feladat, Mozgó elektromos töltésre ható erő (Lorentz-erő)
Hivatkozás(ok):	Feladatok: 2015/január: 4701. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás.

a)

A mágneses térben

v

sebességgel mozgó,

Q

töltésű golyóra ható erő a sebességvektorra is és a mágneses indukcióvektorra is merőleges, nagysága

F = Q B v

. (Kihasználtuk, hogy

B

és

v

merőlegesek egymásra, és az egyértelműség kedvéért feltételezzük, hogy

Q > 0

.)
A golyók sebessége az

R

sugarú karika középpontjának

v_{0}

nagyságú vízszintes sebességéből és a tiszta gördülés

R ω = v_{0}

nagyságú, érintő irányú sebességéből tehető össze (1. ábra). A

P_{1}

pontban ez

v_{1} = 2 v_{0}

nagyságú, a

P_{2}

pontban pedig

v_{2} = \sqrt[]{3} v_{0}

(egy szabályos háromszög kétszeres magasságának megfelelő) nagyságú sebességvektort eredményez, így a kérdéses erők:

\begin{matrix} F_{1} & = Q B v_{1} = 2 Q B v_{0}, \\ F_{2} & = Q B v_{2} = \sqrt[]{3} Q B v_{0} . \end{matrix}

1. ábra

b)

A karika bármely pontjának sebességvektora két vektor (a haladó mozgás és a forgómozgás kerületi sebességének) összegeként állítható elő. A karikához rögzített töltött testre ható mágneses Lorentz-erőt az egyes sebességkomponensekhez tartozó mágneses erők vektori összegeként is megkaphatjuk (szuperpozíció-elv). Tekintsük a karika azon helyzetét, amelyben a

P_{2}

ponthoz tartozó sugár

φ

szöget zár be a függőlegessel, a

P_{1}

-hez tartozó sugár ehhez képest

α

szöggel ,,lemarad'' (2. ábra). Keressük

φ

azon értékét (vagy értékeit), amely(ek)nél az eredő erőnek nincs forgatónyomatéka a karika

O

középpontjára vonatkoztatva.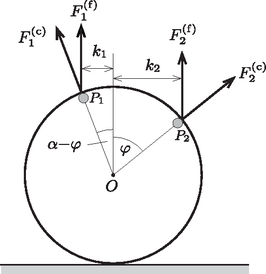

2. ábra

Az érintő irányú sebességvektorokhoz tartozó

F_{1}^{(c)}

és

F_{2}^{(c)}

erők sugár irányúak (centrálisak), az

O

pontra vonatkoztatott forgatónyomatékuk nulla. A vízszintes (transzlációs) sebességnek megfelelő Lorentz-erő függőleges irányú, és a nagysága a karika minden pontjánál ugyanakkora:

\begin{matrix} F_{1}^{(f)} = F_{2}^{(f)} = Q B v_{0} . \end{matrix}

Az erők eredőjének akkor lesz nulla a forgatónyomatéka, ha a megfelelő erőkarok megegyeznek:

\begin{matrix} k_{1} = k_{2}, vagyis sin (α - φ) = sin φ . \end{matrix}

Ebből ‐ trigonometrikus átalakítások után ‐ a

tg (α / 2) = tg φ

egyenlet következik, amelynek megoldása:

\begin{matrix} φ = \frac{α}{2} = 30^{\circ}, vagy φ = 180^{\circ} + \frac{α}{2} = 210^{\circ} . \end{matrix}

Mindkét helyzetben a golyók a karika függőleges átmérőjére nézve szimmetrikusan helyezkednek el. Sebességük nagysága a ,,felső'' helyzetben nagyobb, ilyenkor az eredő erő nagysága

(2 + \sqrt[]{3}) Q v_{0} B

, az ,,alsó'' szimmetrikus helyzetben pedig csak

(2 - \sqrt[]{3}) Q v_{0} B

c)

Tekintsük a karika azon helyzetét, amelyben a

P_{1}

pontba húzott sugár

φ

szöget, a

P_{2}

ponthoz tartozó sugár pedig

φ + α

szöget zár be a függőlegessel (3. ábra). Megmutatjuk, hogy a ponttöltésekre ható mágneses erők hatásvonalainak

P_{3}

metszéspontja tetszőleges

φ

szög esetén a karika és a talaj

P

érintkezési pontjával esik egybe. (Az ábrát szándékosan kicsit eltorzítottuk, nehogy a bizonyítandó állítást a helyes ábráról indoklás nélkül olvassuk le.)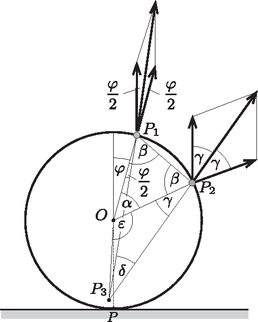

3. ábra

Használjuk ki, hogy az egyes ponttöltésekre ható mágneses erő két komponense (a tiszta gördülés miatt) ugyanakkora, eredőjük tehát felezi a közöttük lévő

φ

, illetve

2 γ = φ + α

nagyságú szöget. Az

O P_{1} P_{2}

háromszög egyenlő szárú, így

\begin{matrix} β = \frac{180^{\circ} - α}{2} . \end{matrix}

P_{1} P_{2} P_{3}

háromszög belső szögeinek összegéből

\begin{matrix} \frac{180^{\circ} - α}{2} - \frac{φ}{2} + \frac{180^{\circ} - α}{2} + \frac{α + φ}{2} + δ = 180^{\circ}, vagyis δ = \frac{α}{2} \end{matrix}

adódik. Ezek szerint (a

P_{1} P_{2}

körívhez tartozó középponti és kerületi szögek tétele alapján) a

P_{3}

pont a karikán helyezkedik el, méghozzá éppen a karika függőleges átmérőjének alsó végpontjánál, hiszen az

O P_{2} P_{3}

háromszög belső szögeinek összegéből (kihasználva, hogy

O P_{3} P_{1} ∢ = φ / 2

\begin{matrix} ε + \frac{φ + α}{2} + \frac{φ}{2} + δ = 180^{\circ}, \end{matrix}

tehát

\begin{matrix} ε + α + φ = 180^{\circ} \end{matrix}

adódik. Ezzel beláttuk, hogy a

P_{3}

pont

P

-vel esik egybe, vagyis a mágneses erők eredője a karika és a talaj érintkezési pontján halad át.

II. megoldás. A karika mozgása minden pillanatban leírható a talaj és a karika érintkezési pontja (a

P

pont) körüli forgómozgással. (Ezen a ponton átmenő és a karika síkjára merőleges tengelyt pillanatnyi forgástengelynek nevezik.) A szögsebesség nagysága nem függ a tengely választásától, értéke bármely tengely, így pl. a karika középpontján átmenő tengely körüli forgásra is

ω = v_{0} / R

.
Jelöljük a

P

pontból

P_{1}

-be és

P_{2}

-be mutató vektorokat (a karika tetszőleges helyzeténél)

r_{1}

-gyel és

r_{2}

-vel, a

P_{1}

és

P_{2}

pontok közötti szakasz felezőpontját pedig

P^{*}

-gal (4. ábra). A

P^{*}

pont a karika

O

középpontjától

R (1 + \sqrt[]{3} / 2)

távolságra helyezkedik el, és a

P

pontból

P^{*}

-ba mutató vektor

\begin{matrix} r^{*} = \frac{r_{1} + r_{2}}{2} \end{matrix}

módon adható meg.

4. ábra

A karika

ω

szögsebessége az ábra síkjára merőleges (tehát

B

-vel párhuzamos) vektor, melynek segítségével a sebességek

\begin{matrix} v_{1} = ω \times r_{1} és v_{2} = ω \times r_{2}, \end{matrix}

a megfelelő Lorentz-erők pedig

\begin{matrix} F_{1} = Q v_{1} \times B = Q (ω \times r_{1}) \times B, illetve F_{2} = Q v_{2} \times B = Q (ω \times r_{2}) \times B . \end{matrix}

Kihasználva, hogy

r_{1,2}

a karika síkjában fekvő vektorok, az egyes erők és az eredőjük így is felírható:

\begin{matrix} F_{1} = Q ω B r_{1}, F_{2} = Q ω B r_{2}, \\ F_{1} + F_{2} = Q ω B (r_{1} + r_{2}) = 2 Q ω B r^{*} . \end{matrix}

a)

A feladat kitűzési ábráján (vagyis a

φ = 0

helyzetben)

| r_{1} | = 2 R

és

| r_{2} | = \sqrt[]{3} R

, így

\begin{matrix} | F_{1} | = 2 Q v_{0} B, illetve | F_{2} | = \sqrt[]{3} Q v_{0} B . \end{matrix}

b)

A mágneses erők eredőjének akkor nincs forgatónyomatéka a karika középpontjára vonatkoztatva, amikor

r^{*}

átmegy az

O

ponton, vagyis amikor

r^{*}

függőleges irányú vektor. Ez két esetben,

φ = - α / 2 = - 30^{\circ}

-nál és

φ = π - α / 2 = - 150^{\circ}

-nál következik be. A töltött golyócskák mindkét helyzetben a függőleges átmérőre nézve szimmetrikusan helyezkednek el. Az eredő erő nagysága

\begin{matrix} | F_{1} + F_{2} | = 2 Q ω B | r^{*} | = Q B v_{0} (2 \pm \sqrt[]{3}) . \end{matrix}

A pozitív előjel a felső, a negatív pedig az alsó szimmetrikus helyzetnek felel meg. Az eredő erő tehát a felső helyzetben lesz nagyobb.

c)

Mivel mind az

F_{1}

, mind pedig az

F_{2}

erő hatásvonala áthalad a

P

ponton, az eredő erő is ezen a ponton halad át, erre a pontra vonatkoztatott forgatónyomatéka a karika tetszőleges helyzetében nulla.