Feladat:	C.1208	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bereczki Zoltán ,  Farkas Dóra ,  Fényes Balázs ,  Gnandt Balázs ,  Hegel Patrik ,  Jójárt Alexandra ,  Telek Máté László
Füzet:	2014/május, 268 - 272. oldal		PDF  |  MathML
Témakör(ök):	C gyakorlat, Vektorok lineáris kombinációi, Középpontos tükrözés, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 2014/január: C.1208

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. A bizonyításban felhasználjuk a vektorok összeadására vonatkozó paralelogramma szabályt, amely miatt $\overrightarrow{LQ}=\overrightarrow{LP}+\overrightarrow{LR}$, illetve $\overrightarrow{LT}=\overrightarrow{LA}+\overrightarrow{LS}$. Felhasználjuk még, hogy az $\overrightarrow{x}$ és $\overrightarrow{y}$ vektor felezőpontjába mutató $\overrightarrow{v}$ vektorra $\overrightarrow{v}=\frac{\overrightarrow{x}+\overrightarrow{y}}{2}$, amiből $\overrightarrow{y}=2\overrightarrow{v}-\overrightarrow{x}$. Azt fogjuk bizonyítani, hogy az $A$ pontot sorra tükrözve a $P$, $Q$, $R$, $S$ és $T$ pontokra, az utolsó tükörkép maga az $A$ pont lesz. Jelölje tehát az $A$ pont tükörképét a $P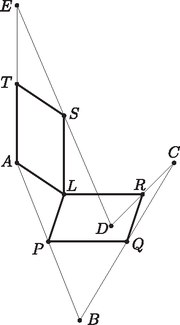$ pontra $B$. Ekkor $\overrightarrow{LB}=2\overrightarrow{LP}-\overrightarrow{LA}$. A $B$ pont tükörképe a $Q$ pontra legyen $C$. Ekkor $\begin{array}{c}{\displaystyle \overrightarrow{LC}=2\overrightarrow{LQ}-\overrightarrow{LB}=2\left(\overrightarrow{LP}+\overrightarrow{LR}\right)-\left(2\overrightarrow{LP}-\overrightarrow{LA}\right)=2\overrightarrow{LR}+\overrightarrow{LA}\mathrm{.}}\end{array}$ A $C$ pont tükörképe az $R$ pontra legyen $D$. Ekkor $\begin{array}{c}{\displaystyle \overrightarrow{LD}=2\overrightarrow{LR}-\overrightarrow{LC}=2\overrightarrow{LR}-\left(2\overrightarrow{LR}+\overrightarrow{LA}\right)=-\overrightarrow{LA}\mathrm{.}}\end{array}$     A $D$ pont tükörképe az $S$ pontra legyen $E$. Ekkor $\begin{array}{c}{\displaystyle \overrightarrow{LE}=2\overrightarrow{LS}-\overrightarrow{LD}=2\overrightarrow{LS}+\overrightarrow{LA}\mathrm{.}}\end{array}$ Végül az $E$ pont tükörképét a $T$ pontra jelölje $F$. Ekkor $\begin{array}{c}{\displaystyle \overrightarrow{LF}=2\overrightarrow{LT}-\overrightarrow{LE}=2\left(\overrightarrow{LA}+\overrightarrow{LS}\right)-\left(2\overrightarrow{LS}+\overrightarrow{LA}\right)=\overrightarrow{LA}\mathrm{.}}\end{array}$ Vagyis $\overrightarrow{LF}=\overrightarrow{LA}$, és így valóban $F\equiv A$, tehát az így kapott $ABCDE$ ötszög megfelelő.   II. megoldás. Az $A$ pont tükörképe a $P$ pontra legyen a $B$ pont, a $B$ pont tükörképe a $Q$ pontra pedig a $C$ pont. Ha létrejön az $ABC$ háromszög, akkor abban az $AB$ oldal felezőpontja $P$, a $BC$ oldalé pedig $Q$, így $PQ\parallel AC$ és $PQ=AC/2$. Mivel $PQRL$ paralelograma, vagyis szemközti oldalai párhuzamosak és egyenlő hosszúak, ezért ebből $LR\parallel AC$ és $LR=AC/2$ következik. Ha nem jön létre háromszög, akkor több eset lehetséges. Az $LSTA$ és a $PQRL$ paralelogrammáknak azonos a körüljárásuk és az $L$ ponton kívül nincs közös részük, ezért az $A$, $P$ és $Q$ pontok csak $APQ$ sorrendben követhetik egymást. Minden esetben a pontok egy egyenesre esnek, így $PQ\parallel AC$, tehát $LR\parallel AC$ is teljesülni fog. Belátjuk, hogy $LR=PQ=AC/2$ is mindig igaz. Legyen $AP=PB=a$ és $BQ=QC=b$. I. eset: $AP=PQ$. Ekkor $Q\equiv B\equiv C$, és így $AC=2PQ$. II.1. eset: $AP>PQ$ és $PQ=AP/2$.     Ekkor $AC=AP=2PQ$. II.2. eset: $PQ<AP/2$.     Ekkor $PQ=PB-QB=a-b$ és $AC=AB-CB=2a-2b$, tehát valóban 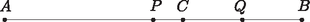$AC=2PQ$. II.3. eset: $AP>PQ>AP/2$.     Ekkor $PQ=PB-QB=a-b$ és $AC=AB-CB=2a-2b$, vagyis $AC=2PQ$.     III. eset: $PQ>AP$.     Itt is teljesül, hogy $AC=2PQ$. Most induljunk el a másik irányba: tükrözzük az $A$ pontot a $T$ pontra, a tükörkép legyen $E$, majd az $E$ pontot az $S$ pontra, a tükörkép legyen $D$. Az $ADE$ háromszögben $TS$ középvonal, így párhuzamos $AD$-vel és feleakkora. Mivel $TS\parallel AL$ és $TS=AL$ is teljesül, ezért $AL\parallel AD$ és $AL=AD/2$, így $L$ az $AD$ felezőpontja. Tehát az $A$ pont tükörképe $L$-re a $D$ pont. Legyen a $D$ pont tükörképe az $R$ pontra a $C\text{'}$ pont. Ha $A$, $L$, $D$ és $R$ nem esnek egy egyenesre, akkor az $ADC\text{'}$ háromszögben $LR$ középvonal, így párhuzamos $AC\text{'}$-vel és feleakkora. Mivel ugyanez igaz az $AC$-re is, ezért $C\equiv C\text{'}$. Ha a négy pont egy egyenesre esik, akkor a pontok sorrendje lehet $RALD$, $ARLD$, $ALRD$ vagy $ALDR$. Minden esetet meg lehet vizsgálni attól függetlenül, hogy valójában létrejöhetnek-e. Mindegyikben megkapjuk, hogy $LR\parallel AC\text{'}$ és feleakkora. Tehát ekkor is $C\equiv C\text{'}$. Két ilyen esetet mutat az alábbi két ábra.       Az így kapott $ABCDE$ négyszög tehát megfelelő. A pontokat megkaphatjuk úgy is, hogy sorban tükrözünk a 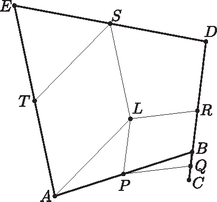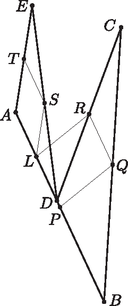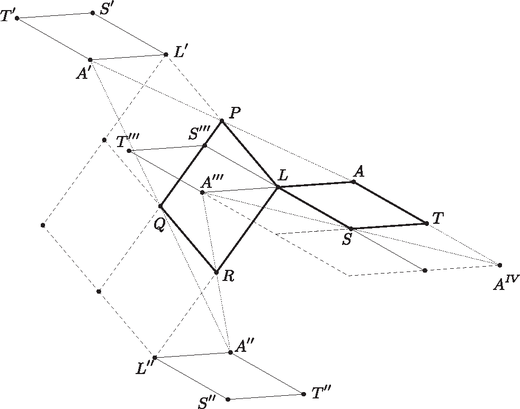$P$, $Q$, $R$, $S$ és $T$ pontokra.   Megjegyzés. Nagyon sokan nem vizsgálták meg a megoldásukban felhasznált háromszögekre (pl. $BCD$, $ABD$ vagy $ACD$) azt, amikor a csúcsaik egy egyenesre esnek. Lásd például az alábbi két elfajuló esetet.         III. megoldás. A feladat lényegében azt mondja, hogy ha az $A$ csúcsot tükrözzük a $P$, $Q$, $R$, $S$, majd $T$ pontra, akkor önmagát kapjuk vissza. Hogy jobban látszódjon a tükrözés, tükrözzük az egész $ALST$ paralelogrammát a pontokra. A paralelogrammán belül is nézzük az $L$ pontot, hiszen az mindkét paralelogrammának csúcsa, így talán könnyebb dolgunk lesz.     Az első tükrözésnél az $L$ tükörképe $L\text{'}$, amiről tudjuk, hogy illeszkedik az $LP$ félegyenesre és $PL=PL\text{'}$. Az $ALST$ képét jelölje $A\text{'}L\text{'}S\text{'}T\text{'}$. Ez az $ALST$-vel egyező állású (vagyis minden oldala párhuzamos annak megfelelő oldalaival), ám körüljárási iránya azzal ellentétes. Ha ezt a paralelogrammát tükrözzük a $Q$ pontra, akkor az eredetivel egyező állású és körüljárású $A\text{'}\text{'}L\text{'}\text{'}S\text{'}\text{'}T\text{'}\text{'}$ paralelogrammát kapjuk, melyben $L\text{'}\text{'}$ illeszkedik a $PQRL$ által meghatározott paralelogramma rácsra, azon belül az $LR$ félegyenesre is és $LR=LR\text{'}\text{'}$. Ebből következik, hogy ha az $A\text{'}\text{'}L\text{'}\text{'}S\text{'}\text{'}T\text{'}\text{'}$ négyszöget az $R$ pontra tükrözzük, akkor $L\text{'}\text{'}$ képe az $L$ pont lesz, valamint az így kapott $A\text{'}\text{'}\text{'}LS\text{'}\text{'}\text{'}T\text{'}\text{'}\text{'}$ paralelogramma az $ALST$-vel egyező állású és ellentétes körüljárású lesz. A továbbiakban vizsgáljuk csak az $A\text{'}\text{'}\text{'}$ pont és tükörképei helyzetét. Ehhez rajzoljuk meg az $ALST$ által meghatározott paralelogramma rácsot. Mivel $A\text{'}\text{'}\text{'}LS\text{'}\text{'}\text{'}T\text{'}\text{'}\text{'}$ az $ALST$-vel egyező állású (és vele egybevágó), így maga is illeszkedik erre a rácsra. Az $A\text{'}\text{'}\text{'}$ pontot az $S$ pontra tükrözve az $A^{\text{<span style="font-style: italic;">IV</span>}}$ pontot kapjuk, amely illeszkedik az $AT$ félegyenesre és $TA=T{A}^{\text{<span style="font-style: italic;">IV</span>}}$. Így nyilván az $A^{\text{<span style="font-style: italic;">IV</span>}}$ tükörképe a $T$ pontra az $A$ pont, tehát az $AA\text{'}A\text{'}\text{'}A\text{'}\text{'}\text{'}{A}^{\text{<span style="font-style: italic;">IV</span>}}$ egy megfelelő ötszög ($A\text{'}\equiv B$, $A\text{'}\text{'}\equiv C$, $A\text{'}\text{'}\text{'}\equiv D$ és $A^{\text{<span style="font-style: italic;">IV</span>}}\equiv E$).