Kezdőlap


Feladat:	B.4581	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Baran Zsuzsanna , Bereczki Zoltán , Di Giovanni Márk , Forrás Bence , Gáspár Attila , Gyulay-Nagy Szuzina , Jenei Dániel Gábor , Kabos Eszter , Lajkó Kálmán , Leipold Péter , Leitereg Miklós , Nagy Gergely , Nagy-György Pál , Nemes György , Sal Kristóf , Schwarz Tamás , Simkó Irén , Williams Kada
Füzet:	2014/április, 223 - 225. oldal		PDF \| MathML
Témakör(ök):	Feladat, Vektorok, Gömbi geometria, Ponthalmazok, Kör (és részhalmaza), mint mértani hely
Hivatkozás(ok):	Feladatok: 2013/november: B.4581

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a két kitérő egyenes $a$ és $b$ , a keresett harmadik egyenes $c$ . Vegyünk fel egy térbeli derékszögű koordinátarendszert úgy, hogy az $x$ tengely essen egybe $a$ -val, a $z$ tengely legyen párhuzamos $b$ -vel, az $y$ tengely egyenese pedig legyen $a$ és $b$ normáltranzverzálisa. Válasszuk meg az egységet úgy, hogy $b$ átmenjen a $(0,1,0)$ ponton (1. ábra). Legyen $U = a \cap c$ és $V = b \cap c$ . Ekkor $U$ koordinátái $(u,0,0)$ , $V$ koordinátái pedig $(0,1, v)$ , ahol $u$ és $v$ valós számok. Az $a$ , $b$ és $c$ egyenesek egy-egy irányvektora 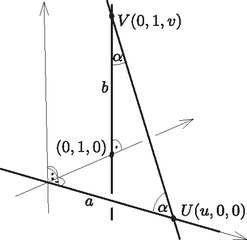$a = (1,0,0)$ , $b = (0,0,1)$ és $c = (- u,1, v)$ .

1. ábra

Két egyenes hajlásszöge vagy megegyezik az irányvektoraik hajlásszögével, vagy azt

180^{\circ}

-ra egészíti ki (2. ábra). Tetszőleges

φ

szög esetén

cos^{2} φ = cos^{2} (180^{\circ} - φ)

, ezért

c

pontosan akkor tesz eleget a feladat feltételeinek, ha

\begin{matrix} cos^{2} α = cos^{2} (a, c) ∢ = cos^{2} (b, c) ∢ \end{matrix}

teljesül. A vektorok szögének koszinuszát viszont a skaláris szorzatukból könnyen kiszámolhatjuk, hiszen tetszőleges

s = (s_{1}, s_{2}, s_{3})

és

t = (t_{1}, t_{2}, t_{3})

vektorok esetén

\begin{matrix} cos (s, t) ∢ = \frac{s t}{| s | | t |} = \frac{s_{1} t_{1} + s_{2} t_{2} + s_{3} t_{3}}{\sqrt[]{s_{1}^{2} + s_{2}^{2} + s_{3}^{2}} \sqrt[]{t_{1}^{2} + t_{2}^{2} + t_{3}^{2}}} . \end{matrix}

2. ábra

Így azt kapjuk, hogy

c

pontosan akkor jó egyenes, ha

\begin{matrix} cos^{2} α = {(\frac{a c}{| a | | c |})}^{2} = {(\frac{b c}{| b | | c |})}^{2}, \end{matrix}

azaz felhasználva, hogy

| a | = | b | = 1

, ha

{(- u)}^{2} = v^{2}

, vagyis ha

u = \pm v

. Ekkor

\begin{matrix} cos^{2} α = \frac{u^{2}}{2 u^{2} + 1} < \frac{1}{2}, \end{matrix}

(1)

vagyis

cos α < 1 / \sqrt[]{2}

, ezért

α > 45^{\circ}

.
Tehát ha

α \leq 45^{\circ}

, akkor nincs a feltételeknek eleget tevő

c

egyenes. Ha viszont

α > 45^{\circ}

, akkor négy megfelelő egyenes van. Ekkor ugyanis az (1) egyenletből

u^{2}

-et kifejezve kapjuk, hogy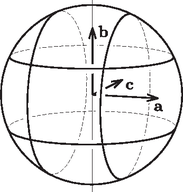

\begin{matrix} u^{2} = \frac{cos^{2} α}{1 - 2 cos^{2} α} > 0, \end{matrix}

ha tehát

\begin{matrix} w = \sqrt[]{\frac{cos^{2} α}{1 - 2 cos^{2} α}}, \end{matrix}

akkor a

(\pm w,0,0)

pontok bármelyikét a

(0,1, \pm w)

pontok bármelyikével összekötő egyenes

α

szöget fog bezárni

a

-val is és

b

-vel is.

II. megoldás. Használjuk az I. megoldás jelöléseit. A feltétel szerint

a

és

c

által bezárt szög, illetve

b

és

c

által bezárt szög is

α

vagy

π - α

. Ábrázoljuk a vektorokat az egységgömbön, azaz egy rögzített egységgömb középpontjából mérjük fel őket és tekintsük a végpontjaikat. Azok a vektorok, amiknek az

a

vektorral bezárt szöge

α

vagy

π - α

, egy

a

és egy

- a

középpontú,

α

sugarú körön helyezkednek el. Hasonlóan, azok a vektorok, amiknek a

b

vektorral bezárt szöge

α

vagy

π - α

, egy

b

és egy

- b

középpontú,

α

sugarú körön vannak. A

c

vektor e két halmaz metszetében van (3. ábra).

3. ábra

A gömbön

a

és

b

távolsága

π / 2

, mert az

a

és

b

egyenesek merőlegesek egymásra. Ha tehát

α < π / 4

, akkor a két halmaznak nincs közös pontja, ezért nem létezik a feltételeknek megfelelő

c

egyenes.
Ha

α = π / 4

, akkor a két halmaznak 4 közös pontja van, továbbá az

a

b

és

c

vektorok egy síkba esnek. Ez azt jelenti, hogy ekkor az

a, b

és

c

egyeneseknek is egy síkba kellene esniük, ami ellentmond annak, hogy

a

és

b

kitérők. Tehát ekkor sincs a feltételeknek eleget tevő egyenes.
Végül, ha

π / 4 < α < π / 2

, akkor a két halmaznak 8 közös pontja van, az

a

b

és

c

vektorok pedig lineárisan függetlenek. Ilyenkor az

a

és

b

egyenesek és a

c

vektor egyértelműen meghatározzák a

c

egyenes helyzetét: az

a

egyenes és a

c

vektor egyértelműen meghatározza az

a

és

c

egyeneseket tartalmazó

S_{a}

síkot, a

b

egyenes és a

c

vektor pedig egyértelműen meghatározza a

b

és

c

egyeneseket tartalmazó

S_{b}

síkot. Az

S_{a}

és

S_{b}

síkok különbözőek, mert

a

és

b

kitérők,

c

pedig e két sík metszésvonala. Mivel az ellentétes irányú

c

irányvektorok ugyanazt a

c

egyenest határozzák meg, ezért ebben az esetben összesen 4, a feltételeknek megfelelő egyenes létezik.
Összefoglalva tehát

α \leq π / 4

esetén 0,

α > π / 4

esetén pedig 4 a két egymásra merőleges kitérő egyenest metsző, mindkettővel

α

szöget bezáró egyeneseknek a száma.
Megjegyzés. Az, hogy a megfelelő egyenesek száma néggyel osztható, egyszerűen belátható. Ha

a

és

b

normáltranzverzálisa az

n

egyenes, az

a

és

n

egyeneseket tartalmazó sík

M_{a}

, a

b

és

c

egyeneseket tartalmazó sík

M_{b}

c

pedig egy a feltételeknek eleget tevő egyenes, akkor

c

-nek

M_{a}

-ra, illetve

M_{b}

-re vonatkozó tükörképei is jó egyenesek, mert az

a

és

b

egyenesek képei önmaguk és a tükrözés szögtartó. Ezért ha az

U

pont

M_{a}

-ra vonatkozó tükörképe

U'

, a

V

pont

M_{b}

-re vonatkozó tükörképe pedig

V'

(4. ábra), akkor az

U V

U V'

U' V

és

U' V'

egyenesek közül bármelyik pontosan akkor tesz eleget a feladat feltételeinek, amikor a három másik.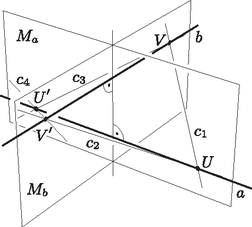

4. ábra