Feladat: B.4562 Korcsoport: 16-17 Nehézségi fok: könnyű
Megoldó(k):  Kocsis Júlia 
Füzet: 2014/április, 216 - 217. oldal  PDF  |  MathML 
Témakör(ök): Feladat, Síkgeometriai bizonyítások, Thalesz tétel és megfordítása, Középponti és kerületi szögek
Hivatkozás(ok):Feladatok: 2013/október: B.4562

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

 
I. megoldás. Legyen F az AC befogó fölé írt Thalész kör középpontja. Mivel a kör érintője merőleges az érintési pontba húzott sugárra, FED∢=90∘, Thalész tétele szerint pedig AEC∢=90∘.
Az FEA és FCD háromszögek egyenlő szárúak, mert FA=FE=FC. Ezért, ha FAE∢=α, akkor FEA∢=α, tehát 90∘-α=FEC∢=FCE∢ (1. ábra). Vagyis
CED∢=FED∢-FEC∢=90∘-(90∘-α)=α
és
ECD∢=FCD∢-ECD∢=90∘-(90∘-α)=α.
Tehát az ECD háromszög D-nél lévő külső szöge EDB∢=CED∢+ECD∢=2α. Az EBD háromszög B-nél lévő szöge
EBD∢=ABC∢=90∘-CAB∢=90∘-α,
E-nél lévő szöge pedig
BED∢=180∘-(EDB∢+EBD∢)=180∘-(2α+90∘-α)=90∘-α.

Vagyis az EBD háromszög E-nél és B-nél lévő szögei megegyeznek, tehát a háromszög egyenlő szárú.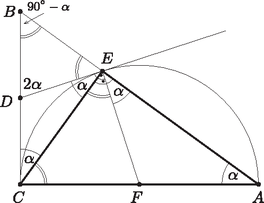
 

1. ábra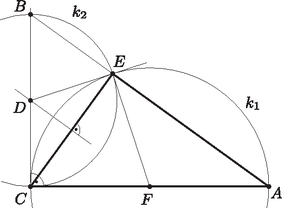
 


2. ábra

 
II. megoldás. Legyen k1 és k2 az AC, illetve a BC befogó Thalész köre. Ekkor Thalész tétele miatt CE merőleges az AB oldalra, ezért Thalész tételének megfordítása miatt a k2 kör is átmegy az E ponton (2. ábra).
Mivel DC merőleges a k1 kör CA átmérőjére, DC a C pontban érinti k1-et. A D pontból k1-hez húzott DC és DE érintők egyenlő hosszúak, ezért D rajta van a CE szakaszfelező merőlegesén. Ugyanakkor a BC szakasz a k2 kör átmérője, ezért a kör CE húrjának felezőmerőlegese ezt az átmérőt a kör középpontjában metszi, így D a k2 középpontja. Tehát DB és DE a k2 kör két sugara, amik egyenlő hosszúak, azaz az EBD háromszög egyenlő szárú.