Feladat: B.4555 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Williams Kada 
Füzet: 2014/április, 211 - 214. oldal  PDF  |  MathML 
Témakör(ök): Feladat, Hossz, kerület, Koszinusztétel alkalmazása, Esetvizsgálat
Hivatkozás(ok):Feladatok: 2013/szeptember: B.4555

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

 
Megoldás. A pontok közötti kétféle távolságot x-szel és y-nal fogjuk jelölni, hiszen nem lesz azonnal világos, hogy melyik hosszúság a nagyobb.
Először tekintsük azokat az elrendezéseket, amelyekben a négy pont között van három olyan, amely egy ABC szabályos háromszöget határoz meg, mondjuk x oldalhosszúságút. A negyedik D pontnak az első háromtól vett távolságai között lesz két egyenlő, ami például AD=BD az általánosság megszorítása nélkül. Ez azt jelenti, hogy D rajta van AB oldalfelező merőlegesén, ami a C csúcson is áthalad.
Ha itt CD=x, akkor D kétféle lehet, az 1. ábra szerint. A bal oldalon szereplő elrendezésben szimmetria miatt
DCA∢=DCB∢=360∘-60∘2=150∘.

1. ábra

Mivel AC=CD, azért x és y egy 150∘-os szárszögű egyenlő szárú háromszög oldalai. A jobb oldali ábrán pedig DCA∢=DCB∢=30∘ és CA=CD=CB, így
CDA∢=CDB∢=180∘-30∘2=75∘
és emiatt ADB∢=2⋅75∘=150∘. Ezzel x és y ismét egy 150∘-os szárszögű egyenlő szárú háromszög oldalai. Tehát mindkét esetben ugyanahhoz az a/b arányhoz jutunk. Ennek kiszámításához alkalmazzuk a koszinusztételt:
a2=b2+b2-2b2cos150∘.
Itt cos150∘=-32 és így a2b2=2+3, ab=2+3.
Ha DA=DB=x, akkor vagy C=D (amit kizárhatunk), vagy pedig D a C pont tükörképe AB-re (2. ábra). Utóbbi esetben x és y egy 2⋅60∘=120∘-os szárszögű egyenlő szárú háromszög oldalai. Legyen P=CD∩AB, ekkor Pitagorasz-tétellel
PC2=AC2-AP2=x2-x24=34x2
(az ábra CD-re szimmetrikus), azaz
y=CD=2⋅PC=2⋅3x24=3⋅x.
A kapott arány tehát ab=3.
 

2. ábra
 

Ha pedig sem DC, sem DA=DB nem lesz x hosszúságú, akkor y=DA=DB=DC, így D az ABC kör középpontja (2. ábra). Ekkor
ADB∢=BDC∢=CDA∢=360∘3=120∘,
tehát x és y az előző esethez hasonlóan egy 120∘-os szárszögű egyenlő szárú háromszög oldalai, a kapott arány tehát az előző esetbeli ab=3.
Mivel másféle elrendezésben nem szerepelhet szabályos háromszög, így a további esetekben feltételezzük, hogy szabályos háromszög nem jön létre.
Induljunk ki egy ABC egyenlő szárú háromszögből. Mivel a negyedik, D pont távolsága A-tól, B-től és C-től kétféle, így D rajta lesz az ABC háromszög egyik oldalfelező merőlegesén (3. ábra). Két esetünkben D rendre az AB=y alap, illetve a BC=x szár felezőmerőlegesén lesz.
Amennyiben DA=DB, akkor DA=DB≠AB=y, mert akkor volna szabályos háromszög, vagyis DA=DB=AC=BC=x. Tekintve, hogy az ACD háromszög sem szabályos, CD=y. Tehát ADBC egy egyenlő átlójú rombusz, vagyis szükségképpen négyzet. A Pitagorasz-tételt az ABC háromszögre alkalmazva y2=x2+x2, ahonnan ab=yx=2.
 

3. ábra

 


4. ábra

 

A legbonyolultabb eset, amikor DB=DC (4. ábra). Mivel a DBC háromszög nem szabályos és BC=x, így DB=DC=y. A DAB háromszög sem szabályos, ezért DA=x. Vegyük észre, hogy az ABD és BDC háromszög oldalegyenlőség miatt egybevágó, amiből ABD∢=BDC∢. Ezt AB=BD=DC-vel összevetve az adódik, hogy ABDC szimmetrikus trapéz. Legyen AD∩BC=P és α=BAD∢. Váltószögek és egyenlő szárú háromszögek miatt
α=BAD∢=BDA∢=DAC∢=ACB∢
és BAC∢=2α=ABC∢, sőt
APB∢=180∘-APC∢=2α.
Ebből adódik, hogy AB=AP=PC=y. Az is kiderült, hogy az ABP és CAB háromszögek hasonlók, amiből ABPB=CAAB. Behelyettesítve
 
a megfelelő értékeket yx-y=xy, szorzással (x>y) y2=x2-xy, majd osztva x2y2-xy-1=0.

A kapott másodfokú egyenlet pozitív gyöke kell nekünk: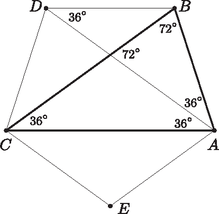
ab=xy=1+52
lesz a megoldás. Tehát a lehetséges a/b hányadosok: 2, 1+52, 3 és 2+3. Mindegyik eset ténylegesen létezik, és előállítja a megadott arányokat. Az utolsó esetben ez például abból látható, hogy az elrendezés a szabályos ötszög egy részeként áll elő (ld. 5. ábra).
 

5. ábra