Feladat:	B.4469	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Medek Ákos ,  Tóth Zsombor
Füzet:	2014/március, 144 - 147. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Algebrai átalakítások, Síkgeometriai bizonyítások, Háromszög területe, Háromszögek nevezetes tételei
Hivatkozás(ok):	Feladatok: 2012/szeptember: B.4469

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Jelölje a szokásos módon az $ABC$ háromszög oldalainak hosszát $a$, $b$ és $c$, szögeit pedig $\alpha$, $\beta$ és $\gamma$. Tetszőleges $P$, $Q$, $R$ pontok esetén legyen $T_{PQR}$ a $PQR$ háromszög területe. Ekkor az ismert területképlet szerint $\begin{array}{c}{\displaystyle 2T_{ABC}=ab\text{sin}\gamma =bc\text{sin}\alpha =ca\text{sin}\beta \mathrm{,}}\end{array}$ továbbá $\begin{array}{c}{\displaystyle 2T_{A_1{B}_{1}C}=C{A}_1\cdot C{B}_1\text{sin}\gamma \mathrm{,}2T_{A_{1}B{C}_1}=B{A}_1\cdot B{C}_1\text{sin}\beta }\end{array}$ és $\begin{array}{c}{\displaystyle 2T_{A{B}_1{C}_1}=A{B}_1\cdot A{C}_1\text{sin}\alpha \mathrm{.}}\end{array}$ A szögfelezőtétel szerint $\frac{B{A}_1}{C{A}_1}=c:b$, továbbá $B{A}_1+C{A}_1=a$, ezért $\begin{array}{c}{\displaystyle B{A}_1=\frac{ac}{b+c}\text{és}C{A}_1=\frac{ab}{b+c}\mathrm{.}}\end{array}$ Hasonlóképpen kapjuk meg az $A{B}_1$, $C{B}_1$, $A{C}_1$ és $B{C}_1$ szakaszok hosszát is (1. ábra). Ezeket felhasználva $\begin{array}{c}{\displaystyle \frac{T_{A_1{B}_{1}C}}{T_{ABC}}=\frac{\frac{ab}{b+c}\cdot \frac{ab}{a+c}\text{sin}\gamma }{ab\text{sin}\gamma }=\frac{ab}{\left(a+c\right)\left(b+c\right)}\mathrm{,}}\end{array}$ és ugyanígy adódik, hogy 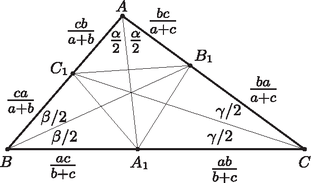$\begin{array}{c}{\displaystyle \frac{T_{A_{1}B{C}_1}}{T_{ABC}}=\frac{ac}{\left(a+b\right)\left(b+c\right)}\text{és}\frac{T_{A{B}_1{C}_1}}{T_{ABC}}=\frac{bc}{\left(a+b\right)\left(a+c\right)}\mathrm{.}}\end{array}$     1. ábra   Azt kell belátnunk, hogy ennek a három törtnek az összege legalább 3/4, mert abból $T_{A_1{B}_1{C}_1}+T_{A_1{B}_{1}C}+T_{A_{1}B{C}_1}+T_{A{B}_1{C}_1}=T_{ABC}$ miatt következik, hogy $\begin{array}{c}{\displaystyle \frac{T_{A_1{B}_1{C}_1}}{T_{ABC}}\le \frac{1}{4}\mathrm{.}}\end{array}$ A bizonyítandó $\begin{array}{c}{\displaystyle \frac{ab}{\left(a+c\right)\left(b+c\right)}+\frac{ac}{\left(a+b\right)\left(b+c\right)}+\frac{bc}{\left(a+b\right)\left(a+c\right)}\ge \frac{3}{4}}\end{array}$ egyenlőtlenséget $4\left(a+b\right)\left(b+c\right)\left(a+c\right)$-vel szorozva, majd egyszerűsítve és rendezve kapjuk, hogy $\begin{array}{c}{\displaystyle a^{2}b+a{b}^2+a^{2}c+a{c}^2+b^{2}c+b{c}^2\ge 6abc\mathrm{.}}\end{array}$ $abc>0$-val való osztás után elegendő megmutatnunk, hogy $\begin{array}{c}{\displaystyle \frac{a}{b}+\frac{b}{a}+\frac{a}{c}+\frac{c}{a}+\frac{b}{c}+\frac{c}{b}\ge 6}\end{array}$ teljesül. Ez viszont igaz, mert tudjuk, hogy bármely pozitív számnak és a reciprokának az összege legalább 2. Az is látszik, hogy egyenlőség csak az $a=b=c$ esetben áll fenn, vagyis ha az $ABC$ háromszög szabályos.   II. megoldás. Használjuk az I. megoldás jelöléseit. Feltehetjük, hogy a háromszög oldalainak hosszára $c\le b\le a$ teljesül. Legyenek az $ABC$ háromszög oldalainak felezőpontjai a 2. ábra szerint $D$, $E$ és $F$. Ismert, hogy $\begin{array}{c}{\displaystyle \frac{T_{DEF}}{T_{ABC}}=\frac{1}{4}\mathrm{,}}\end{array}$ ezért állításunk bizonyításához elegendő megmutatnunk, hogy $T_{DEF}\ge T_{A_1{B}_1{C}_1}$.     2. ábra   Először belátjuk, hogy $T_{D{B}_1{C}_1}\ge T_{A_1{B}_1{C}_1}\mathrm{.}$ Ha $b=c$, akkor $D=A_1$, ezért a két háromszög megegyezik. Ha $b>c$, akkor az I. megoldásban kiszámolt szakaszhosszakat felhasználva kapjuk, hogy $\begin{array}{c}{\displaystyle \frac{A{B}_1}{A{C}_1}=\frac{\frac{bc}{a+c}}{\frac{bc}{a+b}}=\frac{a+b}{a+c}<\frac{b}{c}\mathrm{.}}\end{array}$ Vagyis a $B_1$ pont távolabb van a $BC$ oldaltól, mint a $C_1$ pont, tehát a $G=B_1{C}_1\cap BC$ pontra teljesül, hogy a $GC$ szakasz tartalmazza a $B$ pontot. A $c<b$ feltételből az is következik, hogy $B{A}_1<A_{1}C$, és mivel $D$ felezi a $BC$ szakaszt, azért $B{A}_1<BD\mathrm{.}$ Ha viszont egy szög egyik szárán távolodunk a szög csúcsától, akkor a szög másik szárának egyenesétől is egyre messzebb kerülünk (3. ábra). Ezért $D$ messzebb van a $B_1{C}_1$ egyenestől, mint $A_1$, a $D{B}_1{C}_1$ és $A_1{B}_1{C}_1$ háromszögek közül az első területe a nagyobb, mert a közös oldalukhoz tartozó magasságaik közül is az elsőé a nagyobb.     3. ábra. $O{P}_1<O{P}_2\iff d_1<d_2$   Ugyanígy látható be, hogy a $b\le a$ feltevésből $T_{DE{C}_1}\ge T_{D{B}_1{C}_1}$ következik (ha $D{C}_1\cap AC=H$, akkor a $HC$ szakasz tartalmazza $A$-t és $A{B}_1<B_{1}C$). Végül pedig $DE$ és $AB$ párhuzamossága miatt $T_{DEF}=T_{DE{C}_1}$, s így $\begin{array}{c}{\displaystyle T_{DEF}=T_{DE{C}_1}\ge T_{D{B}_1{C}_1}\ge T_{A_1{B}_1{C}_1}\mathrm{,}}\end{array}$ ami éppen a bizonyítandó állítás.