| Feladat: | C.1139 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Imre Nóra , Lapis Máté Sámuel , Molnár-Sáska Zoltán , Roszjár Lea , Várkonyi Lídia | ||
| Füzet: | 2014/március, 139 - 144. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | C gyakorlat, Egyenlőtlenségek, Derékszögű háromszögek geometriája, Hossz, kerület | ||
| Hivatkozás(ok): | Feladatok: 2012/október: C.1139 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Mivel egy derékszögű háromszög oldalainak hossza pozitív, alkalmazhatjuk rájuk a négyzetes és számtani közép között fennálló egyenlőtlenséget:
A Pitagorasz-tételt szerint . Továbbá tudjuk, hogy , ahol állandó. Ez utóbbiból következik. Helyettesítsük be ezeket az (1) egyenlőtlenségbe: Mivel állandó, az átfogó legalább . Létezik is olyan háromszög, amelynek éppen ekkora az átfogója, ennek a befogóinak hossza: Alkalmazzuk a derékszögű háromszög oldalainak négyzetére a számtani és a mértani közepek közötti egyenlőtlenséget:
A Pitagorasz-tétel szerint , ezt írjuk be a (2) egyenlőtlenségbe: Mindkét oldalhoz -et adva: , Adott esetén ennek akkor van minimuma, amikor a nevezőnek és egyben -nak maximuma. Növeljük az egyik befogót -szel, a másikat pedig csökkentsük -nal (), és nézzük meg, változatlan kerület mellett hogyan változik az átfogó. Ha a két befogó , illetve , akkor kerület mellett az átfogó Azt szeretnénk belátni, hogy , hiszen ekkor az átfogó nagyobb, mint az egyenlő szárú háromszög esetén. Írjuk fel a Pitagorasz-tételt, majd rendezzük a kapott egyenletet: Mivel , és pozitívak, a jobb oldal csak úgy lehet 0, ha , vagyis . Ezzel beláttuk, hogy egyenlő szárú háromszög esetén a legkisebb az átfogó. Ha az átfogó , akkor a befogó , a kerület pedig: , ahonnan A Pitagorasz-tétel miatt . Mivel adott, így és is az. akkor lesz a lehető legnagyobb, ha a négyzete is az: . Ebből adott, tehát és így akkor lesz a legnagyobb, amikor , és egyben felveszi a maximumát. A Thalész-tétel megfordítása miatt a háromszögnek az átfogóval szemközti csúcsa az átfogó Thalész-körén helyezkedhet el. Legyen a átfogóhoz tartozó magasságvonal . Ekkor a háromszög területe , vagyis . Mivel adott, ezért ez akkor lesz a legnagyobb, amikor a lehető legnagyobb, ez pedig akkor következik be, amikor egyben a oldal felező merőlegese is, vagyis amikor a háromszög egyenlő szárú. Egyenlő szárú háromszög esetén pedig a kerület , az átfogó , ami a kerületnek az -szerese. 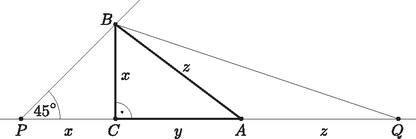 Mivel egyenlő szárú derékszögű háromszög, . Emiatt a csúcs a -val -os szöget bezáró félegyenesen helyezkedik el -tól távolságra, tehát a pont az pont körül sugárral húzott kör és a félegyenes közös pontja. Ezért legalább akkora, mint az pont és a félegyenes távolsága. Így Ebből következik, hogy legkisebb értéke , ami akkor következik be, amikor az középpontú, sugarú kör érinti a félegyenest. Ekkor , és így , vagyis az háromszög egyenlő szárú. Ezt ábrázolva látható, hogy azok az számpárok lesznek egy 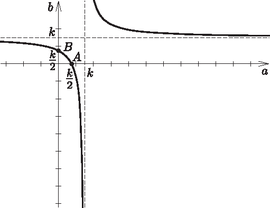 2. ábra 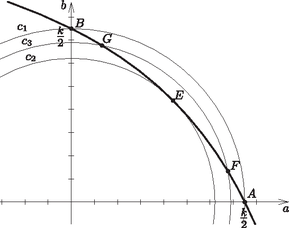 3. ábra Mivel a Pitagorasz tétel szerint , így egy középpontú, sugarú kör és a hiperbola-ív metszéspontjainak koordinátái egy megfelelő ( kerületű) háromszög befogóinak hosszát adják (3. ábra). A értéke kisebb, mint a kör sugara, vagyis , és legalább akkora, mint a kör sugara. (A kör egy ,,köztes'' kört mutat, ahol és két megfelelő háromszög koordinátáit adják.) A kör az pontban érinti a hiperbola-ívet, a szimmetria miatt két koordinátája egyenlő. Tehát értéke egyenlő szárú háromszög esetén lesz minimális, kiszámolható (lásd pl. a IV. megoldást), hogy ekkor . |