Feladat:	B.4490	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ágoston Péter ,  Balogh Tamás ,  Bogár Blanka ,  Fehér Zsombor ,  Fonyó Viktória ,  Gyulay-Nagy Szuzina ,  Herczeg József ,  Janzer Olivér ,  Kúsz Ágnes ,  Machó Bónis ,  Maga Balázs ,  Medek Ákos ,  Nagy Róbert ,  Petrényi Márk ,  Sagmeister Ádám ,  Szabó Attila ,  Szabó Barnabás ,  Szőke Tamás ,  Tardos Jakab ,  Tossenberger Tamás
Füzet:	2014/február, 88 - 92. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Menelaosz-tétel, Szinusztétel alkalmazása
Hivatkozás(ok):	Feladatok: 2012/november: B.4490

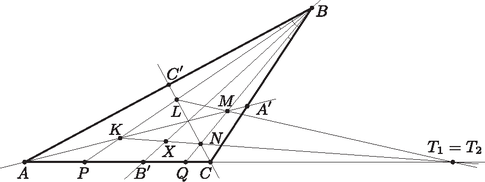
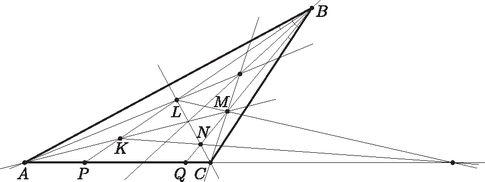
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Legyenek a háromszög szögfelezőinek a szemközti oldalszakaszokkal vett metszéspontja $A\text{'}$, $B\text{'}$, $C\text{'}$, a $KN$ és $BB\text{'}$ egyenes metszéspontja $X$. A megoldásunk során nem előjeles szakaszokkal dolgozunk. A szögekre vonatkozó feltételből következik, hogy az $AC$ egyenesen a pontok sorrendje $A$, $P$, $B\text{'}$, $Q$, $C$ (hiszen $ABP\sphericalangle <ABB\text{'}\sphericalangle$, valamint $CBQ\sphericalangle <CBB\text{'}\sphericalangle$), valamint az, hogy a $BB\text{'}$ nemcsak az $ABC\sphericalangle$, hanem a $PBQ\sphericalangle$ szögfelezője is, hiszen $\begin{array}{c}{\displaystyle PBB\text{'}\sphericalangle =ABB\text{'}\sphericalangle -ABP\sphericalangle =B\text{'}BC\sphericalangle -QBC\sphericalangle =B\text{'}BQ\sphericalangle \mathrm{.}}\end{array}$     Mivel $AA\text{'}$, $BB\text{'}$, $CC\text{'}$ szögfelezők, egy pontban metszik egymást, tehát a $KM$, $BX$ és $NL$ egyenesek is egy pontban metszik egymást, hiszen azonosak az előbb felsorolt egyenesekkel. Így a $BKN$ háromszögre felírható a Ceva-tétel: $\begin{array}{c}{\displaystyle \frac{KL}{LB}\cdot \frac{BM}{MN}\cdot \frac{NX}{XK}=1.}\end{array}$ Messe az $LM$ és $KN$ egyenes az $AC$ oldalegyenesét a $T_1$, illetve a $T_2$ pontban. A Menelaosz-tétel szerint a $BPQ$ háromszögre és a $BP$ és $BQ$ oldalakat metsző $LM$ egyenesre: $\begin{array}{c}{\displaystyle \frac{PL}{LB}\cdot \frac{BM}{MQ}\cdot \frac{Q{T}_1}{T_{1}P}=\mathrm{1,}}\end{array}$ a $BPQ$ háromszögre és a $BP$ és $BQ$ oldalakat metsző $KN$ egyenesre: $\begin{array}{c}{\displaystyle \frac{PK}{KB}\cdot \frac{BN}{NQ}\cdot \frac{Q{T}_2}{T_{2}P}=1.}\end{array}$ Megmutatjuk, hogy $\frac{Q{T}_1}{T_{1}P}=\frac{Q{T}_2}{T_{2}P}$. Mivel $\begin{array}{c}{\displaystyle \frac{PL}{LB}\cdot \frac{BM}{MQ}\cdot \frac{Q{T}_1}{T_{1}P}=\frac{PK}{KB}\cdot \frac{BN}{NQ}\cdot \frac{Q{T}_2}{T_{2}P}\mathrm{,}}\end{array}$ a bizonyítandó állítással ekvivalens a következő: $\begin{array}{c}{\displaystyle \frac{PL}{LB}\cdot \frac{BM}{MQ}=\frac{PK}{KB}\cdot \frac{BN}{NQ}\mathrm{.}}\end{array}$ Mivel a $CC\text{'}$ az $ACB$ szög felezője, a $PCB\sphericalangle$ szögfelezője is, tehát $CL$ szögfelezője a $PCB$ szögnek. Hasonlóan adódik, hogy $AM$ a $QAB\sphericalangle$ szögfelezője, $AK$ a $PAB\sphericalangle$ szögfelezője, $CN$ pedig a $QCB\sphericalangle$ szögfelezője, azaz $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}{\displaystyle \text{ a <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Q</mi><mi>A</mi><mi>B</mi></math> háromszögre:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>Q</mi><mi>M</mi></mrow><mrow><mi>M</mi><mi>B</mi></mrow></mfrac></mrow><mo stretchy="false">=</mo><mrow><mfrac><mrow><mi>Q</mi><mi>A</mi></mrow><mrow><mi>A</mi><mi>B</mi></mrow></mfrac></mrow></math>,}}\hfill \\ {\displaystyle \text{ a <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>P</mi><mi>A</mi><mi>B</mi></math> háromszögre:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>P</mi><mi>K</mi></mrow><mrow><mi>K</mi><mi>B</mi></mrow></mfrac></mrow><mo stretchy="false">=</mo><mrow><mfrac><mrow><mi>P</mi><mi>A</mi></mrow><mrow><mi>A</mi><mi>B</mi></mrow></mfrac></mrow></math>,}}\hfill \\ {\displaystyle \text{ a <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>P</mi><mi>C</mi><mi>B</mi></math> háromszögre:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>P</mi><mi>L</mi></mrow><mrow><mi>L</mi><mi>B</mi></mrow></mfrac></mrow><mo stretchy="false">=</mo><mrow><mfrac><mrow><mi>P</mi><mi>C</mi></mrow><mrow><mi>C</mi><mi>B</mi></mrow></mfrac></mrow></math>,}}\hfill \\ {\displaystyle \text{ a <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Q</mi><mi>C</mi><mi>B</mi></math> háromszögre:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>Q</mi><mi>N</mi></mrow><mrow><mi>N</mi><mi>B</mi></mrow></mfrac></mrow><mo stretchy="false">=</mo><mrow><mfrac><mrow><mi>Q</mi><mi>C</mi></mrow><mrow><mi>C</mi><mi>B</mi></mrow></mfrac></mrow></math>. }}\hfill \end{array}}}\end{array}$ Tehát a bizonyítandó $\frac{PL}{LB}\cdot \frac{BM}{MQ}=\frac{PK}{KB}\cdot \frac{BN}{NQ}$ állítás ekvivalens ezzel: $\begin{array}{c}{\displaystyle \frac{PC}{CB}\cdot \frac{AB}{QA}=\frac{PA}{AB}\cdot \frac{CB}{QC}\mathrm{,}}\end{array}$ átrendezve: $\begin{array}{c}{\displaystyle \frac{AB}{CB}\cdot \frac{AB}{CB}=\frac{PA}{QC}\cdot \frac{QA}{PC}\mathrm{.}}\end{array}$ A szinusztételt felhasználva: $\begin{array}{c}{\displaystyle \frac{AB}{AP}\cdot \frac{QC}{BC}=\frac{\text{sin}APB\sphericalangle \text{sin}QBC\sphericalangle }{\text{sin}ABP\sphericalangle \text{sin}BQC\sphericalangle }=\frac{\text{sin}APB\sphericalangle }{\text{sin}BQC\sphericalangle }\mathrm{,}}\end{array}$ hiszen $ABP\sphericalangle =QBC\sphericalangle$. Hasonlóan: $\begin{array}{c}{\displaystyle \frac{BC}{CP}\cdot \frac{AQ}{AB}=\frac{\text{sin}BPC\sphericalangle \text{sin}ABQ\sphericalangle }{\text{sin}PBC\sphericalangle \text{sin}AQB\sphericalangle }=\frac{\text{sin}BPC\sphericalangle }{\text{sin}AQB\sphericalangle }\mathrm{,}}\end{array}$ hiszen $PBC\sphericalangle =ABC\sphericalangle -ABP\sphericalangle =ABC\measuredangle \sphericalangle -QBC\sphericalangle =ABQ\sphericalangle$. Mivel $APB\sphericalangle ={180}^{\circ }-BPC\sphericalangle$ és $BQC\sphericalangle ={180}^{\circ }-AQB\sphericalangle$, így $\begin{array}{c}{\displaystyle \frac{AB}{AP}\cdot \frac{QC}{BC}=\frac{\text{sin}APB\sphericalangle }{\text{sin}BQC\sphericalangle }=\frac{\text{sin}BPC\sphericalangle }{\text{sin}AQB\sphericalangle }=\frac{BC}{CP}\cdot \frac{AQ}{AB}\mathrm{,}\text{azaz}\frac{AB}{CB}\cdot \frac{AB}{CB}=\frac{PA}{QC}\cdot \frac{QA}{PC}\mathrm{.}}\end{array}$ Ezt kellett belátnunk. Így $\frac{Q{T}_1}{T_{1}P}=\frac{Q{T}_2}{T_{2}P}$. A $T_1$ pont nyilván nem lehet a $PQ$ szakasz belső pontja. Ha $\frac{Q{T}_1}{T_{1}P}>1$, akkor $Q{T}_1>T_{1}P$, tehát $T_1$ a $PQ$ egyenes $P$-t nem tartalmazó félegyenesének eleme. Ha $\frac{Q{T}_1}{T_{1}P}<1$, akkor $Q{T}_1<T_{1}P$, tehát   $T_1$ a $PQ$ egyenes $Q$-t nem tartalmazó félegyenesének eleme. Ha $\frac{Q{T}_1}{T_{1}P}=1$ lenne, akkor $ABP\sphericalangle =\frac{1}{2}ABC\sphericalangle$, ami nem megengedett. Legyen adott $T_1$. Ha $T_1=T_2$, akkor nyilván teljesül, hogy $\frac{Q{T}_1}{T_{1}P}=\frac{Q{T}_2}{T_{2}P}$. Más $T_1$ pontra pedig ez nem teljesül, hiszen $T_2$ ugyanazon a félegyenesen van, mint $T_1$ (tehát vagy a $P$-t vagy a $Q$-t nem tartalmazó $PQ$ félegyenesen). Ekkor a $P$, $Q$, $T_1$ pontok sorrendje adott, az általánosság megszorítása nélkül feltehető, hogy $T_1$ a $PQ$ félegyenes $P$-t nem tartalmazó félegyenesén van, tehát $T_{2}P>Q{T}_2$. Ha $T_2$-t $P$-től (és egyben $Q$-tól) távolítjuk $k$-val, akkor $\begin{array}{c}{\displaystyle \frac{Q{T}_2+k}{T_{2}P+k}=1+\frac{Q{T}_2+k-T_{2}P-k}{T_{2}P+k}<1+\frac{Q{T}_2-T_{2}P}{T_{2}P}=\frac{Q{T}_2}{T_{2}P}\mathrm{,}}\end{array}$ tehát az arány csökken. Hasonlóan látható, hogy ha közelítjük, akkor az arány nő, azaz $\begin{array}{c}{\displaystyle \frac{Q{T}_2-k}{T_{2}P-k}=1+\frac{Q{T}_2-k-T_{2}P+k}{T_{2}P-k}>1+\frac{Q{T}_2-T_{2}P}{T_{2}P}=\frac{Q{T}_2}{T_{2}P}\mathrm{,}}\end{array}$ tehát adott $T_1$-hez csak egy megfelelő $T_2$ van. Ehhez hasonlóan belátható az is, ha a $T_1$ (és egyben a $T_2)$ a $PQ$ egyenes $Q$-t nem tartalmazó félegyenesén van, akkor is csak egy $T_2$ van adott $T_1$-hez. Ezzel a feladat állítását beláttuk.     II. megoldás. Azt fogjuk belátni, hogy az $AL$ és $CM$ egyenesek a $B$-ből induló szögfelezőn metszik egymást, ugyanis ez ekvivalens az eredeti állítással. Ha ugyanis ez valóban teljesül, akkor az $AKL$ és $CNM$ háromszögek egyenesre nézve perspektívek, tehát ekkor pontra nézve is perspektívek, vagyis az $AC$, $KN$, $ML$ egyenesek is egy ponton mennek át (Desargues-tétel).     $AK$, $CN$ és $BE$ szögfelezők. Írjunk fel a trigonometrikus Ceva-tételeket szögekre. A $BL$, $AL$ és $CL$ egyenesek egy ponton mennek át, tehát $\begin{array}{c}{\displaystyle \frac{\text{sin}ABL\sphericalangle \cdot \text{sin}BCL\sphericalangle \cdot \text{sin}CAL\sphericalangle }{\text{sin}BAL\sphericalangle \cdot \text{sin}LCA\sphericalangle \cdot \text{sin}LBC\sphericalangle }=1.}\end{array}$ (1) A $CM$, $AM$ és $BM$ egyenesek is egy ponton mennek át, tehát $\begin{array}{c}{\displaystyle \frac{\text{sin}ABM\sphericalangle \cdot \text{sin}BCM\sphericalangle \cdot \text{sin}CAM\sphericalangle }{\text{sin}BAM\sphericalangle \cdot \text{sin}CBM\sphericalangle \cdot \text{sin}ACM\sphericalangle }=1.}\end{array}$ (2) Azt kell belátnunk, hogy $\begin{array}{c}{\displaystyle \frac{\text{sin}CAL\sphericalangle \cdot \text{sin}ABE\sphericalangle \cdot \text{sin}BCM\sphericalangle }{\text{sin}EBC\sphericalangle \cdot \text{sin}BAL\sphericalangle \cdot \text{sin}ACM\sphericalangle }=1.}\end{array}$ (3) Vegyük észre, hogy $ABE\sphericalangle =ECB\sphericalangle$, mivel $BE$ szögfelező, tehát szinuszuk is egyenlő, így (3)-ból a bizonyítandó állítás: $\begin{array}{c}{\displaystyle \frac{\text{sin}CAL\sphericalangle \cdot \text{sin}BCM\sphericalangle }{\text{sin}BAL\sphericalangle \cdot \text{sin}ACM\sphericalangle }=1.}\end{array}$ (4) Mivel $CL$ szögfelező, $BCL\sphericalangle =LCA\sphericalangle$, emiatt (1)-ből $\begin{array}{c}{\displaystyle \frac{\text{sin}ABL\sphericalangle \cdot \text{sin}CAL\sphericalangle }{\text{sin}BAL\sphericalangle \cdot \text{sin}LBC\sphericalangle }=1.}\end{array}$ (5) Mivel $AM$ szögfelező, $BAM\sphericalangle =CAM\sphericalangle$, emiatt (2)-ből $\begin{array}{c}{\displaystyle \frac{\text{sin}ABM\sphericalangle \cdot \text{sin}BCM\sphericalangle }{\text{sin}CBM\sphericalangle \cdot \text{sin}ACM\sphericalangle }=1.}\end{array}$ (6) Tudjuk továbbá azt is, hogy $ABL\sphericalangle =CBM\sphericalangle$ és $ABM\sphericalangle =CBL\sphericalangle$, tehát ezek szinusza is egyenlő. Az (5) és (6) egyenleteket összeszorozzuk, ekkor megkapjuk (4)-et: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{\text{sin}ABL\sphericalangle \cdot \text{sin}CAL\sphericalangle }{\text{sin}BAL\sphericalangle \cdot \text{sin}LBC\sphericalangle }\cdot \frac{\text{sin}ABM\sphericalangle \cdot \text{sin}BCM\sphericalangle }{\text{sin}CBM\sphericalangle \cdot \text{sin}ACM\sphericalangle }}& {\displaystyle =\mathrm{1,}}\hfill \\ \hfill {\displaystyle \frac{\text{sin}CAL\sphericalangle }{\text{sin}BAL\sphericalangle }\cdot \frac{\text{sin}BCM\sphericalangle }{\text{sin}ACM\sphericalangle }}& {\displaystyle =1.}\hfill \end{array}}$ Tehát teljesül a feladat állítása.   Megjegyzés. A feladat projektív geometriai eszközökkel is megoldható. Ha a beírt kör középpontja $I$, és a $BA$, $BP$, $BI$, $BQ$, $BC$ egyeneseket rendre $a$, $p$, $i$, $q$, $c$-vel jelöljük, akkor $\begin{array}{c}{\displaystyle \left(I\mathrm{,}A\mathrm{,}K\mathrm{,}M\right)=\left(i\mathrm{,}a\mathrm{,}p\mathrm{,}q\right)=\left(i\mathrm{,}c\mathrm{,}q\mathrm{,}p\right)=\left(I\mathrm{,}C\mathrm{,}N\mathrm{,}L\right)}\end{array}$ (ahol a zárójelek a megfelelő kettősviszonyokat jelölik). Az $I$, $A$, $K$, $M$ és az $I$, $C$, $N$, $L$ pontnégyesek tehát perspektívek, és ezért az $AC$, $KN$ és $ML$ egyenesek egy ponton mennek át.