Feladat:	B.4468	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Nagy-György Zoltán
Füzet:	2014/február, 86. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Thalesz tétel és megfordítása, Körérintők
Hivatkozás(ok):	Feladatok: 2012/szeptember: B.4468

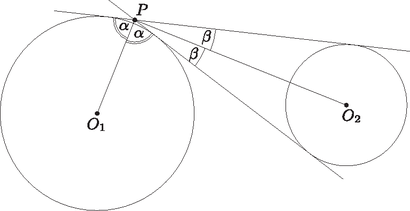
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. A körök közös belső érintői a külső érintőket két-két pontban metszik. A bizonyítandó állítást úgy is fogalmazhatjuk, hogy ezen négy pont mindegyike a körök középpontjait összekötő szakasz, mint átmérő fölé írt körvonalra esik. Szimmetria okok miatt ezt elegendő a négy metszéspont egyikéről belátnunk.     Legyen ez a metszéspont $P$, a körök középpontjai pedig legyenek $O_1$ és $O_2$. Egy körhöz bármely külső pontból húzott két érintő a pontot a kör középpontjával összekötő egyenesre nézve szimmetrikusan helyezkedik el, ezért $O_{1}P$, illetve $O_{2}P$ szögfelezők, vagyis az ábrán azonosan jelölt szögek egyenlők. Mindkét kör a közös külső érintőnek ugyanazon az oldalán van, ezért $2\alpha +2\beta ={180}^{\circ }$, vagyis $\alpha +\beta ={90}^{\circ }$. Tehát az $O_{1}P{O}_2$ szög derékszög, ami Thalész tétele szerint pontosan akkor teljesül, ha $P$ az $O_1{O}_2$ átmérőjű körvonalra esik.