Kezdőlap


Feladat:	B.4485	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Seress Dániel
Füzet:	2014/január, 26 - 27. oldal		PDF \| MathML
Témakör(ök):	Feladat, Számtani-mértani egyenlőtlenségek, Síkgeometriai számítások trigonometria nélkül, Terület, felszín
Hivatkozás(ok):	Feladatok: 2012/november: B.4485

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. A négyzet négy csúcsa közül kettő a háromszögnek ugyanarra az oldalára esik, a háromszög másik két oldalán pedig egy-egy csúcsa kell, hogy legyen a négyzetnek. Feltehetjük, hogy az $A B C$ háromszög oldalain az ábrán látható módon helyezkednek el az $X Y Z V$ négyzet csúcsai, esetleg az $X$ csúcs egybeeshet $A$ -val, vagy az $Y$ csúcs $B$ -v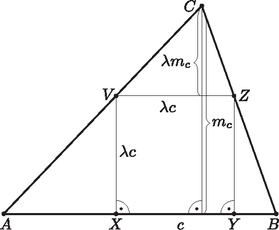el.

A négyzet

V Z

oldala párhuzamos az

A B

egyenessel, ezért az

A B C

és a

V Z C

háromszögek hasonlók. Legyen a hasonlóság aránya

λ

. Ekkor ha akkor a négyzet oldalainak hossza

λ c

, s ha az

A B C

háromszög

C

-hez tartozó magasságának hossza

m_{c}

, akkor a

V Z C

háromszög

C

-hez tartozó magasságának hossza

λ m_{c}

. A négyzet

V X

oldala párhuzamos a háromszögek

C

-hez tartozó magasságaival, ezért

\begin{matrix} m_{c} = λ m_{c} + V X = λ m_{c} + λ c, vagyis λ = \frac{m_{c}}{m_{c} + c}, \end{matrix}

és ezért

0 < λ < 1

.
Legyen az

A B C

háromszög területe

T

. Ekkor

m_{c} = 2 T / c

, tehát

\begin{matrix} λ = \frac{m_{c}}{m_{c} + c} = \frac{2 T}{2 T + c^{2}} . \end{matrix}

Ebből kapjuk, hogy

\begin{matrix} 1 - λ = \frac{c^{2}}{2 T + c^{2}} . \end{matrix}

Ezeket felhasználva a négyzet és az

A B C

háromszög területének aránya

\begin{matrix} \frac{{(λ c)}^{2}}{T} & = 2 λ^{2} \frac{c^{2}}{2 T} = 2 λ \frac{2 T}{2 T + c^{2}} \cdot \frac{c^{2}}{2 T} = 2 λ \frac{c^{2}}{2 T + c^{2}} = \\ = 2 λ (1 - λ) \leq 2 {(\frac{λ + (1 - λ)}{2})}^{2} = \frac{1}{2}, \end{matrix}

ahol a becslésnél a számtani és a mértani közepek közti egyenlőtlenséget használtuk (ezt megtehettük, hiszen

λ

és

1 - λ

is pozitív). Ebben egyenlőség akkor áll fenn, ha

λ = 1 / 2

. Ez pontosan akkor teljesül, ha

\begin{matrix} \frac{2 T}{2 T + c^{2}} = \frac{1}{2}, \end{matrix}

azaz ha

c^{2} = 2 T

, vagyis

c = m_{c}

.
A négyzet tehát a háromszög területének legfeljebb a felét fedheti le, s pontosan akkor fedi le a felét, ha a háromszög egyik magasságának hossza megegyezik a hozzá tartozó oldal hosszával, és a négyzet egyik oldala a háromszögnek ezen az oldalán van.