Feladat:	B.4480	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Schwarcz Tamás
Füzet:	2014/január, 25 - 26. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Hozzáírt körök, Beírt kör, Középvonal
Hivatkozás(ok):	Feladatok: 2012/október: B.4480

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.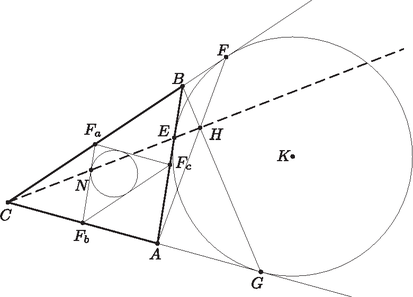   Megoldás. Jelöljük a háromszög oldalait és félkerületét a szokásos módon $a$, $b$, $c$, $s$ betűkkel. Külső pontból a körhöz húzott érintőszakaszok egyenlők, továbbá tudjuk, hogy a hozzáírt körhöz a legtávolabbi csúcsból húzott érintőszakaszok hossza $s$. Ezek alapján $\begin{array}{c}{\displaystyle AE=AG=CG-CA=s-b\mathrm{.}}\end{array}$ Ugyanezzel a gondolatmenettel $\begin{array}{c}{\displaystyle BE=BF=CF-BC=s-a\mathrm{.}}\end{array}$     1. ábra   A $H$ pont akkor és csak akkor van rajta a $CE$ egyenesen, ha az $AF$, $BG$ és $CE$ egyenesek egy pontban metszik egymást. Alkalmazzuk Ceva tételének megfordítását az $ABC$ háromszögre és az oldalegyenesein fekvő $E$, $F$ és $G$ pontokra. A három egyenes pontosan akkor metszi egymást egy pontban, ha $\begin{array}{c}{\displaystyle \frac{BF}{FC}\cdot \frac{CG}{GA}\cdot \frac{AE}{EB}=1.}\end{array}$ Ez akkor is fennáll, ha előjeles szakaszokkal számolunk; pontosan két szakasz ($BF$ és $GA$) előjele lesz negatív. Az eddigiek alapján $CG=CF$, $AE=AG$, továbbá $BE=BF$, tehát a hányadosok előjeles szorzata valóban $1$. Így a $H$ pont rajta van a $CE$ egyenesen. Belátjuk még, hogy az $N$ pont is rajta van a $CE$ egyenesen. Az $F_a{F}_b{F}_c$ háromszög hasonló az $ABC$ háromszöghöz és oldalai, megfelelő szakaszai feleakkorák. Mivel $F_a{F}_c=\frac{b}{2}$, a kerület fele pedig $\frac{s}{2}$, az $F_b$ pontból húzott érintőszakasz $\frac{s-b}{2}$. Az $ABC$ háromszögnek az $F_b{F}_{a}C$ háromszög a $C$ pontból felére kicsinyített képe. Beláttuk, hogy az $F_{b}N$ szakasz éppen fele olyan hosszúságú, mint az $AE$ szakasz, tehát az $E$ pont képe az $N$ pont, az $N$ pont a $CE$ szakasz felezőpontja. A $H$, $E$ és $N$ pontok tehát valóban egy egyenesen vannak.