Feladat:	B.4463	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Lőrinczy Zsófia
Füzet:	2014/január, 20. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Kombinatorikus geometria síkban, Diofantikus egyenletek
Hivatkozás(ok):	Feladatok: 2012/szeptember: B.4463

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Megmutatjuk, hogy rajzolható ilyen téglalap. Legyen a rácspontok távolsága egységnyi. Ekkor a téglalap vízszintes oldalán egységnyi a pontok távolsága, függőleges oldalán pedig $\sqrt[]{3}$ egység. Jelölje a vízszintes oldal hosszát $m$, a függőlegesét $n\sqrt[]{3}$, ahol $n$ és $m$ pozitív egész számok. A téglalap kerületén lévő pontok száma ekkor $2\left(m+n\right)$. A téglalap belsejében azokon a vízszintes rácspont egyeneseken, amelyek nem rácspontban metszik a függőleges oldalakat $m$ pont van, és $n$ ilyen egyenes van. Így ezeknek a pontoknak a száma 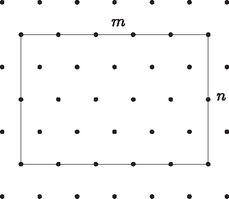$m\cdot n$.     Azokon a vízszintes rácspont egyeneseken, amelyek rácspontokban metszik a függőleges oldalakat $m-1$ belső pont van és $n-1$ ilyen egyenes van. Így ezeknek a pontoknak a száma $\left(m-1\right)\cdot \left(n-1\right)$. A téglalap belsejében tehát $m\cdot n+\left(m-1\right)\cdot \left(n-1\right)=2mn-m-n+1$ rácspont található. A feltételünk: $2\left(m+n\right)=2mn-m-n+1$, vagyis $2mn-3m-3n+1=0$. 2-vel szorozva és szorzattá alakítva: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 4mn-6m-6n+2}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle \left(2m-3\right)\left(2n-3\right)-9+2}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle \left(2m-3\right)\left(2n-3\right)}& {\displaystyle =7.}\hfill \end{array}}$ Itt $2m-3=1$ és $2n-3=7$, vagy fordítva. Tehát a feltételnek megfelelő téglalap oldalai $m=2$ és $n=5$, vagy $m=5$ és $n=2$. Mindkét téglalap határán és belsejében is 14 fa található.