Kezdőlap


Feladat:	B.4356	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Sagmeister Ádám
Füzet:	2012/december, 540. oldal		PDF \| MathML
Témakör(ök):	Feladat, Háromszögek hasonlósága, Síkgeometriai bizonyítások, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 2011/április: B.4356

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Egyenlő szárú háromszögből legfeljebb három ilyen lehet, ezekre a feladat állítása triviálisan teljesül (ha a háromszögek nem szabályosak, akkor a három harmadik csúcs nem esik egy egyenesbe, szabályos háromszög pedig csak egy van a kívánt tulajdonsággal).
A továbbiakban feltesszük, hogy háromszögeink nem egyenlő szárúak; ekkor a számuk pontosan hat, jelölje a harmadik csúcsaikat rendre

C_{1}

C_{2}

C_{3}

C_{4}

C_{5}

és

C_{6}

az ábrán látható módon. A háromszögek hasonlóak, ezért a hat háromszög szögei megegyeznek. Szokás szerint jelöljük az eredeti háromszögben a

C_{1} A B

szöget

α

-val, az

A B C_{1}

szöget

β

-val és 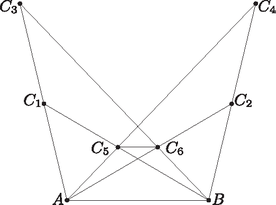a

B C_{1} A

szöget

γ

-val.

Mivel a háromszögek egymással egybevágó, az

A B

felező merőlegesére szimmetrikus párokba sorolhatók,

C_{1} C_{2}

C_{3} C_{4}

és

C_{5} C_{6}

párhuzamosak az

A B

-vel és

A B C_{2} C_{1}

A B C_{4} C_{3}

A B C_{6} C_{5}

húrtrapéz, és így

C_{1} C_{2} C_{4} C_{3}

C_{1} C_{5} C_{6} C_{2}

és

C_{3} C_{5} C_{6} C_{4}

is. A hasonlóság miatt

A B C_{3} ∢ = A B C_{6} ∢ = γ

. A párhuzamosság miatt így a

C_{5} C_{6} C_{3} ∢

γ

. A

C_{3} C_{1} B ∢

B C_{1} A ∢

kiegészítő szöge, ezért

C_{3} C_{1} B ∢ = 180^{\circ} - γ

. Ebből következik, hogy a

C_{3} C_{1} C_{5} C_{6}

négyszögben a szemközti szögek összege

180^{\circ}

, vagyis a négyszög húrnégyszög. A szimmetria miatt ugyanez igaz a

C_{2} C_{4} C_{5} C_{6}

négyszögre is. Tehát a

C_{3} C_{1} C_{5} C_{6}

és

C_{1} C_{5} C_{6} C_{2}

húrnégyszögek három közös csúccsal rendelkeznek, és (például a szimmetria miatt) a többi csúcs is az ezen három pontból alkotott háromszög köré írt körre illeszkedik.