Feladat:	B.4400	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Weimann Richárd
Füzet:	2012/március, 156 - 157. oldal		PDF  |  MathML
Témakör(ök):	Kocka, Feladat, Pitagorasz-tétel alkalmazásai, Másodfokú (és arra visszavezethető) egyenletek
Hivatkozás(ok):	Feladatok: 2011/november: B.4400

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.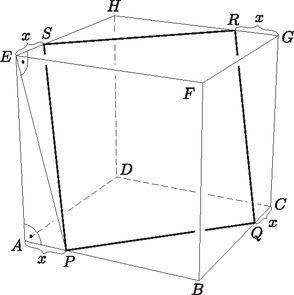   Megoldás. Megmutatjuk, hogy belefér a négyzet a kockába. Jelöljük az egységkocka csúcsait az ábrán látható módon. Rögzítsünk egy $0<x<1$ távolságot, és vegyük fel az $AB$, $BC$, $GH$ és $HE$ éleken azokat a $P$, $Q$, $R$ és $S$ pontokat, amelyekre $AP=CQ=GR=ES=x$. Ekkor a kocka szimmetriája miatt $PQ=RS$ és mindkét szakaszt merőlegesen felezi a $BDHF$ sík, tehát a $PQRS$ négyszög téglalap.     Pithagorasz tétele segítségével az $x$ függvényében könnyen megadhatjuk a téglalap oldalainak hosszát. A $PBQ$ és az $EAP$ háromszögek nyilván derék szögűek, ezért $P{Q}^2=P{B}^2+B{Q}^2=2{\left(1-x\right)}^2$ és $P{E}^2=A{E}^2+A{P}^2=1+x^2$. A kocka $HE$ éle merőleges az $ABFE$ lapra, ezért $PES\sphericalangle ={90}^{\circ }$, tehát $\begin{array}{c}{\displaystyle P{S}^2=P{E}^2+E{S}^2=1+2x^2\mathrm{.}}\end{array}$ Ha tehát $x$-et növeljük, akkor $PQ$ csökken, $PS$ pedig nő. Egy téglalapba írható legnagyobb négyzet oldalának hossza megegyezik a téglalap nem hosszabb oldalának hosszával. Ezért a $PQRS$ téglalapba írható négyzet akkor lesz a legnagyobb, ha $PQ=PS$ teljesül. Ekkor $\begin{array}{c}{\displaystyle 2{\left(1-x\right)}^2=1+2x^2\mathrm{,}\text{azaz}x=\frac{1}{4}\mathrm{.}}\end{array}$ Ebben az esetben $\begin{array}{c}{\displaystyle PQ=PS=\sqrt[]{\frac{9}{8}}=\frac{3\sqrt[]{2}}{4}\approx 1\mathrm{,}06>1\mathrm{,}05.}\end{array}$ Tehát ha a $P$, $Q$, $R$ és $S$ pontokat a megfelelő élek negyedelőpontjainak választjuk, akkor a kocka és a $PQRS$ sík metszetében elfér egy $1\mathrm{,}05\times 1\mathrm{,}05$-ös négyzet.   Megjegyzés. Megmutatható, hogy a megoldásban konstruált $\frac{3\sqrt[]{2}}{4}$ oldalú négyzetnél nagyobb négyzet már nem fér el az egységkockában. Ennek belátása azonban jóval nehezebb feladat, mint magának a négyzetnek a megtalálása.