Feladat:	B.4349	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Dudás Zsolt
Füzet:	2012/március, 144 - 146. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Jensen-féle egyenlőtlenség, Síkgeometriai számítások trigonometriával
Hivatkozás(ok):	Feladatok: 2011/március: B.4349

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.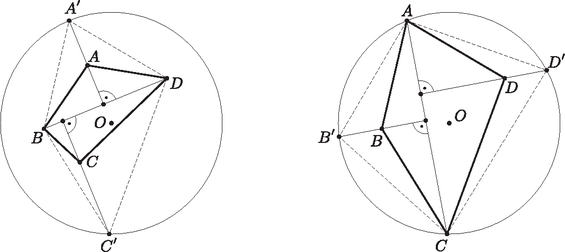   Megoldás. Amennyiben a konvex négyszög valamelyik csúcsa a körlemez belsejében helyezkedik el, a négyszög oldalait lehet úgy növelni, hogy a csúcsokat a körívre visszük ki oly módon, hogy az adott belső csúcson át nem menő átlóra merőleges, az adott pontra illeszkedő félegyenes és a körvonal metszéspontja lesz az új csúcs.     Pitagorasz-tétellel azonnal látható, hogy ezekben az esetekben a két csatlakozó oldal hossza nem csökken. Elegendő tehát húrnégyszögekre bizonyítani az állítást. Írjuk fel a négyszög területét az átlókkal és az oldalakkal is. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_{ABCD}}& {\displaystyle =T_{ABC}+T_{ACD}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{ef\text{sin}\phi }{2}}& {\displaystyle =\frac{ab\text{sin}\beta }{2}+\frac{cd\text{sin}\delta }{2}\mathrm{,}}\hfill \end{array}}$ ahol $\phi$ az átlók szöge, $\beta =ABC\sphericalangle$, $\delta =CDA\sphericalangle$; $a$, $b$, $c$, $d$ a húrnégyszög oldalainak, $e$ és $f$ pedig az átlóinak a hossza. A húrnégyszög szemközti szögei kiegészítő szögek, szinuszaik megegyeznek, továbbá felhasználjuk a kerületi szögek szinusza és a hozzájuk tartozó húrok hossza közötti összefüggést: $\begin{array}{c}{\displaystyle \frac{ef\text{sin}\phi }{2}=\frac{ab\text{sin}\beta }{2}+\frac{cd\text{sin}\delta }{2}=\left(ab+cd\right)\frac{\text{sin}\beta }{2}=\left(ab+cd\right)\frac{e}{4R}\mathrm{.}}\end{array}$ A másik átlóval is két háromszögre bontva a négyszöget: $\begin{array}{c}{\displaystyle T_{ABCD}=\left(bc+da\right)\frac{f}{4R}\mathrm{.}}\end{array}$ A két képlet összeszorzásával: $\begin{array}{c}{\displaystyle T_{ABCD}^2={\left(\frac{ef\text{sin}\phi }{2}\right)}^2=\left(ab+cd\right)\left(bc+ad\right)\frac{ef}{16R^2}\mathrm{.}}\end{array}$ Egyszerűsítve $ef$-fel, felhasználva, hogy $R=1$, továbbá alkalmazva a számtani és mértani közép közötti egyenlőtlenséget: $\begin{array}{c}{\displaystyle \frac{ef\text{sin}{}^2\phi }{4}\ge 2\sqrt[]{abcd}\cdot 2\sqrt[]{abcd}\frac{1}{16}=\frac{abcd}{4}\mathrm{.}}\end{array}$ Azt kaptuk, hogy $\begin{array}{c}{\displaystyle \frac{ef\text{sin}{}^2\phi }{4}\ge \frac{abcd}{4}\mathrm{.}}\end{array}$ A húrnégyszög átlói legfeljebb akkorák, mint a kör átmérői, továbbá $\text{sin}\phi \le 1$, tehát $abcd\le 4$. Egyenlőség csak abban az esetben lehetséges, ha mindkét átló átmérő és ${90}^{\circ }$-os szöget zárnak be egymással, azaz a négyszög négyzet. 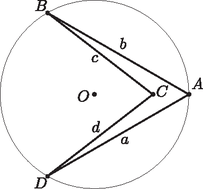  Megjegyzés. Az állítás csak konvex négyszögre igaz, mert legyenek például a mellékelt konkáv négyszög oldalai $a=b=\sqrt[]{3}$, $c=d=\sqrt[]{2}$. Ekkor $\begin{array}{c}{\displaystyle a\cdot b\cdot c\cdot d={\left(\sqrt[]{3}\right)}^2{\left(\sqrt[]{2}\right)}^2=6.}\end{array}$