Feladat:	B.4370	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ágoston Péter ,  Baráti László ,  Bogár Blanka ,  Damásdi Gábor ,  Dinev Georgi ,  Dudás Zsolt ,  Frittmann Júlia ,  Gyarmati Máté ,  Lenger Dániel ,  Maga Balázs ,  Nagy Róbert ,  Perjési Gábor ,  Schulz Vera Magdolna ,  Simig Dániel ,  Strenner Péter ,  Szabó Attila ,  Szilágyi Gergely Bence ,  Tossenberger Tamás ,  Vajda Balázs ,  Zilahi Tamás
Füzet:	2012/február, 91 - 92. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Beírt kör, Síkgeometriai bizonyítások, Egyenlőtlenségek
Hivatkozás(ok):	Feladatok: 2011/május: B.4370

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.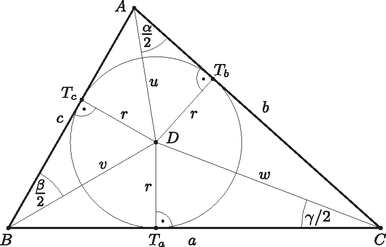   Megoldás. Legyen a beírt kör középpontja $D$, a beírt kör érintési pontjai $T_a$, $T_b$, $T_c$, sugara $r$. Tudjuk, hogy $D{T}_{b}A$, $D{T}_{a}C$ és $D{T}_{c}B$ derékszögű háromszögek, és $D$ a szögfelezők metszéspontja. Tehát $\frac{r}{u}=\text{sin}\frac{\alpha }{2}$, $\frac{r}{v}=\text{sin}\frac{\beta }{2}$ és $\frac{r}{w}=\text{sin}\frac{\gamma }{2}$.   Az általánosság megsértése nélkül feltehetjük, hogy $a\ge b\ge c$. Mivel a háromszögben nagyobb oldallal szemben nagyobb szög van, $\alpha \ge \beta \ge \gamma$. Ebből $\frac{\alpha }{2}\ge \frac{\beta }{2}\ge \frac{\gamma }{2}$. Tudjuk továbbá, hogy $0\le \frac{\alpha }{2}\mathrm{,}\frac{\beta }{2}\mathrm{,}\frac{\gamma }{2}\le \frac{\pi }{2}$. A szinusz-függvény szigorúan monoton nő a $[0;\frac{\pi }{2}]$ intervallumon, így $\begin{array}{c}{\displaystyle \text{sin}\frac{\alpha }{2}\ge \text{sin}\frac{\beta }{2}\ge \text{sin}\frac{\gamma }{2}\mathrm{.}}\end{array}$ Tehát $\frac{r}{u}\ge \frac{r}{v}\ge \frac{r}{w}$, vagyis $\frac{1}{u}\ge \frac{1}{v}\ge \frac{1}{w}$. A rendezési tétel alapján: $\begin{array}{c}{\displaystyle \frac{a}{u}+\frac{b}{v}+\frac{c}{w}\ge \frac{a}{v}+\frac{b}{w}+\frac{c}{u}\text{és}\frac{a}{u}+\frac{b}{v}+\frac{c}{w}\ge \frac{a}{w}+\frac{b}{u}+\frac{c}{v}\mathrm{,}}\end{array}$ amiből ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 3\cdot \left(\frac{a}{u}+\frac{b}{v}+\frac{c}{w}\right)}& {\displaystyle \ge \left(\frac{a}{u}+\frac{b}{v}+\frac{c}{w}\right)+\left(\frac{a}{v}+\frac{b}{w}+\frac{c}{u}\right)+\left(\frac{a}{w}+\frac{b}{u}+\frac{c}{v}\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle 3\cdot \left(\frac{a}{u}+\frac{b}{v}+\frac{c}{w}\right)}& {\displaystyle \ge \left(a+b+c\right)\cdot \left(\frac{1}{u}+\frac{1}{v}+\frac{1}{w}\right)\mathrm{.}}\hfill \end{array}}$ Ezzel beláttuk az állítást.