Kezdőlap


Feladat:	B.4368	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ágoston Péter , Bősze Zsuzsanna , Bunth Gergely , Dinev Georgi , Győrfi Mónika , Homonnay Bálint , Kenéz Balázs , Lenger Dániel , Sagmeister Ádám , Strenner Péter , Tekeli Tamás , Tran Trong Hoang Tuan , Weisz Gellért , Zahemszky Péter , Zsakó László
Füzet:	2012/január, 23 - 25. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Súlypont, Műveletek helyvektorok koordinátáival
Hivatkozás(ok):	Feladatok: 2011/május: B.4368

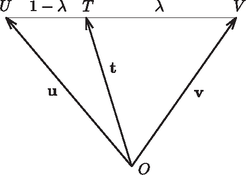
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Ismert, hogy ha az

U V

szakasz végpontjainak helyvektora

u

és

v

, akkor a szakasz tetszőleges

T

pontjának helyvektora

t = λ u + (1 - λ) v

alakban írható, ahol a

0 \leq λ \leq 1

számra

λ \cdot U T = (1 - λ) \cdot T V

teljesül.

1. ábra

2. ábra

Legyen

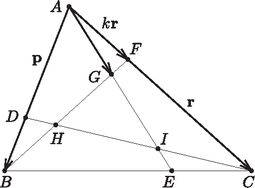
A D : D B = B E : E C = C F : F A = (1 - k) : k

, ekkor a feltétel szerint

k \neq \frac{1}{2}

. Ha bevezetjük az

\vec{A B} = p

és

\vec{A C} = r

jelöléseket, akkor

\vec{A E} = k p + (1 - k) r

és

\vec{A F} = k r

(2. ábra). Mivel a

G

pont rajta van az

A E

szakaszon, van olyan

α

szám, amelyre

\vec{A G} = α \vec{A E} = α (k p + (1 - k) r)

. Másrészt

G

B F

szakasz belső pontja, tehát létezik olyan

β

szám, amelyre

\begin{matrix} \vec{A G} = β \vec{A B} + (1 - β) \vec{A F} = β p + (1 - β) k r . \end{matrix}

\vec{A G}

kétféle felírását egyenlővé téve, majd rendezve kapjuk, hogy

\begin{matrix} α (k p + (1 - k) r) & = β p + (1 - β) k r, \\ (α k - β) p & = ((1 - β) k - α (1 - k)) r . \end{matrix}

Mivel

p

és

r

nem párhuzamos vektorok, ez csak akkor teljesülhet, ha mindkét oldalon 0 az együttható, azaz ha

α k = β

és

(1 - β) k = α (1 - k)

. Ebből az egyenletrendszerből kapjuk, hogy

α = \frac{k}{(k^{2} - k + 1)}

. Vagyis

\begin{matrix} \vec{A G} = α (k p + (1 - k) r) = \frac{k^{2}}{k^{2} - k + 1} p + \frac{k - k^{2}}{k^{2} - k + 1} r . \end{matrix}

(1)

Mivel a

\vec{B H}

és

\vec{H I}

vektorok ugyanazzal az eljárással állíthatók elő a

\vec{B C}

és

\vec{B A}

, illetve a

\vec{C A}

és

\vec{C B}

vektorokból, mint az

\vec{A G}

vektor az

\vec{A B}

és

\vec{A C}

vektorokból, azért

\begin{matrix} \vec{B H} & = \frac{k^{2}}{k^{2} - k + 1} \vec{B C} + \frac{k - k^{2}}{k^{2} - k + 1} \vec{B A}, & (2) \\ \vec{C I} & = \frac{k^{2}}{k^{2} - k + 1} \vec{C A} + \frac{k - k^{2}}{k^{2} - k + 1} \vec{C B} . & (3) \end{matrix}

Ezek után a két háromszög súlypontjának egybeesését már egyszerű számolással igazolhatjuk. Valamely

O

pontból indítsunk helyvektorokat. Az

A

B

és

C

pontok helyvektorait jelölje rendre

a

b

és

c

. Ekkor az

A B C

háromszög súlypontjának helyvektora

(a + b + c) / 3

. Megmutatjuk, hogy ugyanez a

G H I

háromszög súlypontjának helyvektora is, amiből következik, hogy a két súlypont egybeesik.
Mivel

u = b - a

és

v = c - a

, az (1) egyenlőséget felhasználva kapjuk, hogy

\begin{matrix} \vec{O G} & = a + \vec{A G} = a + \frac{k^{2}}{k^{2} - k + 1} (b - a) + \frac{k - k^{2}}{k^{2} - k + 1} (c - a) = \\ = \frac{k^{2} - 2 k + 1}{k^{2} - k + 1} a + \frac{k^{2}}{k^{2} - k + 1} b + \frac{k - k^{2}}{k^{2} - k + 1} c . \end{matrix}

A (2) és (3) egyenlőségekből pedig

\begin{matrix} \vec{O H} & = \frac{k - k^{2}}{k^{2} - k + 1} a + \frac{k^{2} - 2 k + 1}{k^{2} - k + 1} b + \frac{k^{2}}{k^{2} - k + 1} c, \\ \vec{O I} & = \frac{k^{2}}{k^{2} - k + 1} a + \frac{k - k^{2}}{k^{2} - k + 1} b + \frac{k^{2} - 2 k + 1}{k^{2} - k + 1} c \end{matrix}

következik. Ezért

\begin{matrix} \frac{\vec{O G} + \vec{O H} + \vec{O I}}{3} = \frac{a + b + c}{3}, \end{matrix}

ami éppen a bizonyítandó állítás.

Zsakó László
dolgozatát felhasználva

Megjegyzések.

1. A

k \neq \frac{1}{2}

feltételt látszólag nem használtuk ki. A különböző, vektorokra vonatkozó egyenlőségek

k = \frac{1}{2}

esetén is érvényesek, azonban ekkor a

G, H

és

I

pontok mind egybeesnek az

A B C

háromszög súlypontjával, tehát nem jön létre valódi

G H I

háromszög. Persze a feladat állítása igaz abban a formában, hogy az elfajuló

G H I

háromszög súlypontja megegyezik

A B C

súlypontjával.
2. Feladatunkat tulajdonképpen számolás nélkül is megoldhatjuk, felhasználva a következő tételt.

Ha az

A B C

háromszög csúcsainak helyvektorai

a, b

és

c

, akkor a háromszög síkjában lévő tetszőleges pont helyvektora egyértelműen felírható

α a + β b + γ c

alakban, ahol

α + β + γ = 1

A következőképpen okoskodhatunk. Az

A E

és

B F

egyenesek metszéspontjának helyvektora egyértelműen felírható

α a + β b + γ c

alakban, ahol

α + β + γ = 1

. Itt az

α

β

γ

együtthatók csak a

k

értékétől függenek. Ezeket akár ki is számolhatnánk, de ez teljesen felesleges, hiszen szimmetria okok miatt a másik két metszéspont helyvektora

γ a + α b + β c

, illetve

β a + γ b + α c

lesz. Ezek alapján a

G H I

háromszög súlypontjának helyvektora

\begin{matrix} \frac{(α a + β b + γ c) + (β a + γ b + α c) + (γ a + α b + β c)}{3} = \frac{a + b + c}{3} \end{matrix}

valóban megegyezik az

A B C

háromszög súlypontjának helyvektorával.