Feladat:	B.4351	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Perjési Gábor ,  Sieben Bertilla
Füzet:	2012/január, 16 - 19. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Részhalmazok, Elsőfokú (és arra visszavezethető) egyenletrendszerek
Hivatkozás(ok):	Feladatok: 2011/március: B.4351

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.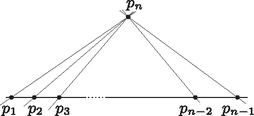   I. megoldás. A halmaz elemei legyenek $p_1\mathrm{,}\text{...}\mathrm{,}{p}_n$, a kiválasztott részhalmazok pedig $L_1\mathrm{,}\text{...}\mathrm{,}{L}_m$. Ha valamelyik $p_i$ csak egyetlen $L_j$-ben szerepel, akkor a feltételek szerint abban a részhalmazban az összes elemnek szerepelnie kell, további részhalmaz pedig nem lehet kiválasztva, vagyis ekkor $m=1$. Tegyük fel tehát, hogy minden $p_i$ legalább két $L_j$-ben szerepel.   1. ábra   Minden $p_i$ elemhez rendeljünk hozzá egy $m$ tagú ${\text{<span style="font-weight: bold;">v</span>}}_i=\left(v_1^i\mathrm{,}{v}_2^i\mathrm{,}\text{...}\mathrm{,}{v}_m^i\right)$ számsorozatot, amelynek $j$-edik tagja 1, ha $p_i\in L_j$, egyébként pedig 0. Ha $\text{<span style="font-weight: bold;">x</span>}=\left(x_1\mathrm{,}\text{...}\mathrm{,}{x}_m\right)$ és $\text{<span style="font-weight: bold;">y</span>}=\left(y_1\mathrm{,}\text{...}\mathrm{,}{y}_m\right)$ két $m$-tagú valós számsorozat, $\alpha$ pedig tetszőleges valós szám, akkor legyen $\begin{array}{c}{\displaystyle \text{<span style="font-weight: bold;">x</span>}+\text{<span style="font-weight: bold;">y</span>}=\left(x_1+y_1\mathrm{,}\text{...}\mathrm{,}{x}_m+y_m\right)\mathrm{,}\alpha \text{<span style="font-weight: bold;">x</span>}=\left(\alpha x_1\mathrm{,}\text{...}\mathrm{,}\alpha x_m\right)\mathrm{,}\langle \text{<span style="font-weight: bold;">x</span>}\mathrm{,}\text{<span style="font-weight: bold;">y</span>}\rangle =x_1{y}_1+\text{...}+x_m{y}_m\mathrm{.}}\end{array}$ Ezek a műveletek a térbeli vektorok összeadásának, számmal való szorzásának és skaláris szorzatának természetes általánosításai. Könnyen meggondolható, hogy az összeadás kommutativitásán és asszociativitásán túl még a következő, a vektorműveleteknél megszokott azonosságok is érvényesek: $\begin{array}{c}{\displaystyle \langle \text{<span style="font-weight: bold;">x</span>}\mathrm{,}\text{<span style="font-weight: bold;">y</span>}\rangle =\langle \text{<span style="font-weight: bold;">y</span>}\mathrm{,}\text{<span style="font-weight: bold;">x</span>}\rangle \mathrm{,}\langle \alpha \text{<span style="font-weight: bold;">x</span>}\mathrm{,}\text{<span style="font-weight: bold;">y</span>}\rangle =\alpha \langle \text{<span style="font-weight: bold;">x</span>}\mathrm{,}\text{<span style="font-weight: bold;">y</span>}\rangle \mathrm{,}\langle \text{<span style="font-weight: bold;">x</span>}+\text{<span style="font-weight: bold;">y</span>}\mathrm{,}\text{<span style="font-weight: bold;">z</span>}\rangle =\langle \text{<span style="font-weight: bold;">x</span>}\mathrm{,}\text{<span style="font-weight: bold;">z</span>}\rangle +\langle \text{<span style="font-weight: bold;">y</span>}\mathrm{,}\text{<span style="font-weight: bold;">z</span>}\rangle \mathrm{.}}\end{array}$ Mivel a feladat feltétele szerint bármely két különböző elem pontosan egy kiválasztott részhalmazban szerepel együtt, azért $i\ne j$ esetén $\langle {\text{<span style="font-weight: bold;">v</span>}}_i\mathrm{,}{\text{<span style="font-weight: bold;">v</span>}}_j\rangle =1$. Feltevésünk szerint pedig minden kiválasztott részhalmaz legalább két elemű, tehát minden $i$-re a $v_j^i$ számok közt legalább kettő darab 1-es szerepel, azaz $\langle {\text{<span style="font-weight: bold;">v</span>}}_i\mathrm{,}{\text{<span style="font-weight: bold;">v</span>}}_i\rangle \ge 2$. Ezek alapján, ha ${\alpha }_1\mathrm{,}\text{...}\mathrm{,}{\alpha }_n$ olyan valós számok, melyekre ${\alpha }_1{\text{<span style="font-weight: bold;">v</span>}}_1+\text{...}+{\alpha }_n{\text{<span style="font-weight: bold;">v</span>}}_n=\text{<span style="font-weight: bold;">0</span>}=\left(\mathrm{0,}\text{...}\mathrm{,0}\right)$, akkor ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 0}& {\displaystyle =\langle \text{<span style="font-weight: bold;">0</span>}\mathrm{,}\text{<span style="font-weight: bold;">0</span>}\rangle =\langle {\sum }_{i=1}^n{\alpha }_i{\text{<span style="font-weight: bold;">v</span>}}_i\mathrm{,}{\sum }_{i=1}^n{\alpha }_i{\text{<span style="font-weight: bold;">v</span>}}_i\rangle ={\sum }_{i=1}^n{\alpha }_i^2\langle {\text{<span style="font-weight: bold;">v</span>}}_i\mathrm{,}{\text{<span style="font-weight: bold;">v</span>}}_i\rangle +2{\sum }_{1\le i<j\le n}{\alpha }_i{\alpha }_j\langle {\text{<span style="font-weight: bold;">v</span>}}_i\mathrm{,}{\text{<span style="font-weight: bold;">v</span>}}_j\rangle =}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={\sum }_{i=1}^n{\alpha }_i^2\left(\langle {\text{<span style="font-weight: bold;">v</span>}}_i\mathrm{,}{\text{<span style="font-weight: bold;">v</span>}}_i\rangle -1\right)+\left({\sum }_{i=1}^n{\alpha }_i^2+2{\sum }_{1\le i<j\le n}{\alpha }_i{\alpha }_j\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={\sum }_{i=1}^n{\alpha }_i^2\left(\langle {\text{<span style="font-weight: bold;">v</span>}}_i\mathrm{,}{\text{<span style="font-weight: bold;">v</span>}}_i\rangle -1\right)+{\left({\sum }_{i=1}^n{\alpha }_i\right)}^2\mathrm{,}}\hfill \end{array}}$ ami $\langle {\text{<span style="font-weight: bold;">v</span>}}_i\mathrm{,}{\text{<span style="font-weight: bold;">v</span>}}_i\rangle -1>0$ miatt csak úgy teljesülhet, ha ${\alpha }_1=\text{...}={\alpha }_n=0$. Az ${\alpha }_1{\text{<span style="font-weight: bold;">v</span>}}_1+\text{...}+{\alpha }_n{\text{<span style="font-weight: bold;">v</span>}}_n=\text{<span style="font-weight: bold;">0</span>}$ feltétel tagonként egy-egy lineáris egyenletet jelent az ${\alpha }_1\mathrm{,}\text{...}\mathrm{,}{\alpha }_n$ ismeretlenekre nézve: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle {\alpha }_1{v}_1^1+{\alpha }_2{v}_1^2\text{...}+{\alpha }_n{v}_1^n}\hfill & \hfill {\displaystyle =}& {\displaystyle \mathrm{0,}}\hfill \\ \hfill {\displaystyle {\alpha }_1{v}_2^1+{\alpha }_2{v}_2^2\text{...}+{\alpha }_n{v}_2^n}\hfill & \hfill {\displaystyle =}& {\displaystyle \mathrm{0,}}\hfill \\ \hfill {\displaystyle ⋮}\hfill & \hfill {\displaystyle }& {\displaystyle }\hfill \\ \hfill {\displaystyle {\alpha }_1{v}_m^1+{\alpha }_2{v}_m^2\text{...}+{\alpha }_n{v}_m^n}\hfill & \hfill {\displaystyle =}& {\displaystyle 0.}\hfill \end{array}}}\end{array}$ Ennek az $m$ darab egyenletből álló egyenletrendszernek tehát csak egyetlen megoldása van, mégpedig az ${\alpha }_1=\text{...}={\alpha }_n=0$. Megmutatjuk, hogy ez csak akkor lehetséges, ha $m\ge n$. Valóban, ha $m<n$ lenne, vagyis az egyenletek száma kisebb lenne az ismeretlenek számánál, akkor az egyenletrendszernek végtelen sok megoldása lenne. Ekkor ugyanis így okoskodhatnánk: ha ${\alpha }_n$ minden egyenletben 0 együtthatóval szerepel, akkor értékét tetszőlegesen megválaszthatjuk. Ha valamelyik egyenletben nem 0 az együtthatója, akkor abból az egyenletből ${\alpha }_n$ kifejezhető a többi ismeretlen segítségével. Ezt a többi egyenletbe beírva kapunk egy $m-1$ egyenletből álló, $n-1$ ismeretlent tartalmazó lineáris egyenletrendszert, ahol az egyenlőségek jobb oldalán ismét csak 0-k állnak. Ezt ismételgetve végül az egyenletrendszert egyetlen egyenletre redukálhatjuk, amelyben legalább két ismeretlen szerepel, ennek viszont nyilván végtelen sok megoldása van. II. megoldás. Jelöljük halmazunkat $\text{P}$-vel, a kiválasztott részhalmazok halmazát pedig $\text{L}$ -lel. Feladatunk valójában a véges geometriák témakörébe tartozik, ezért az ott szokásos elnevezéseket fogjuk használni. A továbbiakban $\text{P}$ elemeit pontoknak, $\text{L}$ elemeit pedig egyeneseknek nevezzük. Ha feltesszük, hogy $\text{L}$ legalább kételemű, akkor a $\left(\text{P}\mathrm{,}\text{L}\right)$ párra teljesülnek a következők: 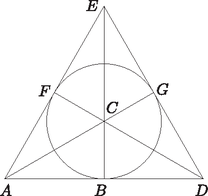$\left(i\right)$ bármely két különböző ponthoz pontosan egy olyan egyenes van, amely őket tartalmazza, $\left(ii\right)$ minden egyenes legalább két pontot tartalmaz, $\left(iii\right)$ legalább két egyenes van.   2. ábra   Az ilyen struktúrát lineáris térnek nevezik. Feladatunk tehát annak belátása, hogy bármely lineáris térben az egyenesek száma legalább annyi, mint a pontok száma. (Ez a lineáris terekre vonatkozó alapvető egyenlőtlenség, melyet De Bruijn‐Erdős egyenlőtlenségnek neveznek, mivel az első bizonyítások e két matematikustól származnak. Az itt közölt bizonyítás megtalálható Kiss Gy. ‐ Szőnyi T.: Véges geometriák című könyvében.) A továbbiakban tegyük fel, hogy $\text{P}=\left\{p_1\mathrm{,}{p}_2\mathrm{,}\text{...}\mathrm{,}{p}_n\right\}$, $\text{L}=\left\{L_1\mathrm{,}{L}_2\mathrm{,}\text{...}\mathrm{,}{L}_m\right\}$ és jelölje $n_i$ a $p_i$ ponton átmenő egyenesek számát $i=\mathrm{1,2,}\text{...}\mathrm{,}n$ esetén, $j=\mathrm{1,2,}\text{...}\mathrm{,}m$ esetén pedig $m_j$ az $L_j$ elemszámát, azaz a $j$-edik egyenesre illeszkedő pontok számát. Ezekre az értékekre egyszerű leszámlálás segítségével felírhatunk három egyenlőséget. Ha az illeszkedő pont‐egyenes párokat először úgy számoljuk össze, hogy megnézzük, hogy egy rögzített ponton hány egyenes megy át, másodjára pedig úgy, hogy megszámoljuk, hogy egy rögzített egyenesre hány pont illeszkedik, akkor a kétféle leszámlálás eredményének meg kell egyeznie, ezért $\begin{array}{c}{\displaystyle \sum _{i=1}^n{n}_i=\sum _{j=1}^m{m}_j\mathrm{.}}\end{array}$ (1) Ugyanilyen módszerrel kétféleképpen leszámolva az illeszkedő pontpár‐egyenes rendezett hármasokat, felhasználva, hogy két különböző pontnak egyértelműen létezik összekötő egyenese, a következő egyenlőséget kapjuk: $\begin{array}{c}{\displaystyle n\left(n-1\right)=\sum _{j=1}^m{m}_j\left(m_j-1\right)\mathrm{.}}\end{array}$ (2) Ha pedig egy $p_i$ pontot fixálunk és az (1) egyenlőséget csak az azon átmenő egyenesekre alkalmazzuk, akkor az $\begin{array}{c}{\displaystyle n-1=\sum _{p\in L_j\in \text{L}}^{}\left(m_j-1\right)}\end{array}$ (3) egyenlőséghez jutunk. Ez szemléletesen azt tükrözi, hogy a $p_i$ pont minden további ponttal egy egyértelmű egyenessel van összekötve. Ha $m>n$, akkor készen vagyunk. Tegyük fel, hogy $m\le n$. Azt kell belátnunk, hogy ekkor itt egyenlőség áll fenn. Először megmutatjuk, hogy ha a $p_i$ pont nincs rajta az $L_j$ egyenesen, akkor $n_i\ge m_j$, és egyenlőség pontosan akkor áll, ha minden $p_i$-n átmenő egyenes metszi $L_j$-t. Ez abból következik, hogy $p_i$-t össze tudjuk kötni $L_j$ minden pontjával, s az így kapott $m_j$ darab egyenes páronként különböző lesz, mert két különböző pontnak egyértelműen létezik összekötő egyenese. Ha egyenlőség áll, akkor pedig $p_i$-n át nem is megy több egyenes. Mivel $n\ge m$ és $n_i\ge m_j$ minden nem-illeszkedő $\left(p_i\mathrm{,}{L}_j\right)$ pont‐egyenes párra, így $n_i\left(n-m_j\right)\ge m_j\left(m-n_i\right)$, azaz $\begin{array}{c}{\displaystyle \frac{n_i}{m-n_i}\ge \frac{m_j}{n-m_j}}\end{array}$ teljesül minden nem-illeszkedő $\left(p_i\mathrm{,}{L}_j\right)$ pont‐egyenes párra. Adjuk össze ezeket az egyenlőtlenségeket minden ilyen párra. Ha a bal oldalakat pontról pontra összeadjuk, akkor a következőt kapjuk: $\begin{array}{c}{\displaystyle \sum _{p_i\notin L_j}^{}\frac{n_i}{m-n_i}=\sum _{i=1}^n\sum _{j:p_i\notin L_j}^{}\frac{n_i}{m-n_i}=\sum _{p=1}^n{n}_i\mathrm{,}}\end{array}$ (4) mivel minden $p_i$ ponthoz pontosan $m-n_i$ olyan egyenes található, amely őt nem tartalmazza. Hasonlóan, ha a jobb oldalakat egyenesről egyenesre adjuk össze, akkor azt kapjuk, hogy $\begin{array}{c}{\displaystyle \sum _{i:p_i\notin L_j}^{}\frac{m_j}{n-m_j}=\sum _{j=1}^m{m}_j\mathrm{.}}\end{array}$ Vagyis a (4) egyenlőtlenség miatt $\begin{array}{c}{\displaystyle \sum _{i=1}^n{n}_i\ge \sum _{j=1}^m{m}_j\mathrm{,}}\end{array}$ itt viszont az (1) egyenlőség miatt egyenlőségnek kell fennállnia. Ez viszont csak úgy lehet, ha $m=n$, ami éppen a bizonyítandó állítás.   Megjegyzés. Ha az egyenlőség esetét tovább vizsgáljuk, akkor azt kapjuk, hogy valamennyi $\left(p_i\mathrm{,}{L}_j\right)$ nem-illeszkedő pont‐egyenes párra az $n_i=m_j$ egyenlőségnek is teljesülni kell. Ez azt jelenti, hogy $m=n$ esetén a lineáris tér bármely két egyenese metszi egymást. Ha van olyan egyenes, amely két pontból áll, akkor nem nehéz belátni, hogy a lineáris terünk csak az 1. ábrán látható lehet. Itt $L_i=\left\{p_i\mathrm{,}{p}_n\right\}$ ha $1\le i<n$, és $L_n=\left\{p_1\mathrm{,}{p}_2\mathrm{,}\text{...}\mathrm{,}{p}_{n-1}\right\}$. Ha viszont minden egyenes legalább három pontból áll, akkor struktúránk ún. véges projektív sík lesz. Erre a legegyszerűbb példa a 2. ábrán látható Fano-sík. Ebben az esetben $\text{P}=\left\{A\mathrm{,}B\mathrm{,}C\mathrm{,}D\mathrm{,}E\mathrm{,}F\mathrm{,}G\right\}$, az egyenesek pedig $\left\{A\mathrm{,}B\mathrm{,}D\right\}$, $\left\{B\mathrm{,}C\mathrm{,}E\right\}$, $\left\{C\mathrm{,}D\mathrm{,}F\right\}$, $\left\{D\mathrm{,}E\mathrm{,}G\right\}$, $\left\{E\mathrm{,}F\mathrm{,}A\right\}$, $\left\{F\mathrm{,}G\mathrm{,}B\right\}$ és $\left\{G\mathrm{,}A\mathrm{,}C\right\}$.