Feladat:	B.4314	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Weiler Virág
Füzet:	2011/május, 286 - 287. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Körök, Pont körüli forgatás, Koszinusztétel alkalmazása
Hivatkozás(ok):	Feladatok: 2010/december: B.4314

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.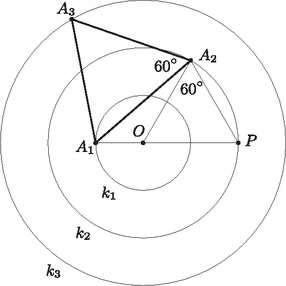   Megoldás. A körök legyenek $k_1$, $k_2$ és $k_3$, közös középpontjuk $O$, a három kiválasztott pont pedig rendre $A_1$, $A_2$ és $A_3$ (1. ábra).   1. ábra   Mivel $A_1{A}_2{A}_3$ szabályos háromszög, van egy olyan $A_2$ körüli ${60}^{\circ }$-os (pozitív vagy negatív irányú) $\phi$ forgatás, amely az $A_3$ pontot $A_1$-be viszi. Ha ennél a $\phi$ forgatásnál $O$ képe a $P$ pont, akkor az $A_{2}OP$ háromszög szabályos, ezért $OP=O{A}_2=2$, vagyis $P$ rajta van a $k_2$ körön. A $k_3$ kör $\phi$-nél kapott $k_3\text{'}$ képe tehát egy $P$ középpontú, 3 sugarú olyan kör, amely áthalad az $A_1$ ponton. Vagyis $A_1$ közös pontja a $k_1$ és $k_3\text{'}$ köröknek. De mivel $\begin{array}{c}{\displaystyle PO+O{A}_1=2+1=3=P{A}_1\mathrm{,}}\end{array}$ az $O$ pont rajta van a $P{A}_1$ szakaszon ‐ ellenkező esetben ugyanis a háromszög-egyenlőtlenség miatt $PO+O{A}_1>P{A}_1$ lenne. Tehát az $A_{2}P{A}_1$ szög megegyezik a ${60}^{\circ }$-os $A_{2}PO$ szöggel. A $A_{2}P{A}_1$ háromszögben $A_{2}P=2$ és $P{A}_1=3$, vagyis a koszinusztétel szerint a háromszög harmadik oldala 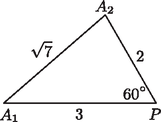$\begin{array}{c}{\displaystyle A_2{A}_1=\sqrt[]{A_2{P}^2+P{A}_1^2-2\cdot A_{2}P\cdot P{A}_1\cdot \text{cos}{60}^{\circ }}=\sqrt[]{7}\mathrm{.}}\end{array}$   2. ábra   Tehát a keresett szabályos háromszög oldala csak $\sqrt[]{7}$ lehet. Az eddigiekből az is könnyen látható, hogy ilyen háromszög valóban létezik.