Feladat: B.4305 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Ágoston Péter ,  Beleznay Soma ,  Herczeg József ,  Kiss Robin ,  Lenger Dániel ,  Perjési Gábor ,  Sieben Bertilla ,  Simig Dániel ,  Veitz Kristóf Tamás ,  Viharos Andor 
Füzet: 2011/május, 284 - 286. oldal  PDF  |  MathML 
Témakör(ök): Térgeometriai bizonyítások, Feladat, Konstruktív megoldási módszer
Hivatkozás(ok):Feladatok: 2010/november: B.4305

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

 
Megoldás. Megmutatjuk, hogy a keresett érték [3n/2].
Egy S sík pontosan akkor metszi a gúla valamelyik élét, ha az él két végpontja S két különböző oldalán helyezkedik el. A gúla alaplapjának A síkját S valamely e egyenesben metszi. Ha az e által meghatározott két A-beli nyílt félsík a gúla csúcsai közül k, illetve ℓ darabot tartalmaz, ahol k≤ℓ, akkor k+ℓ≤n és egyenlőség csak akkor van, ha e egyetlen csúcsot sem tartalmaz. Ezért k≤n/2 mindig teljesül. Ekkor S az alaplap élei közül legfeljebb 2k darabot metsz, mert minden e-t metsző él egyik végpontja a k darab csúcs közül kerül ki és minden csúcsban két él találkozik. A gúla odalélei közül S annak megfelelően metsz k, ℓ vagy 0 darabot, hogy a gúla csúcsa a sík valamelyik oldalán van, vagy illeszkedik S-re.
Tehát S a gúla élei közül legfeljebb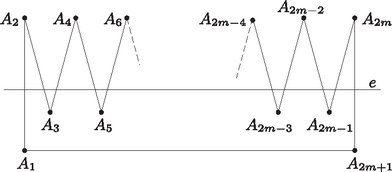
2k+ℓ=k+(k+ℓ)≤k+n≤3n/2
darabot metsz, s mivel a metszéspontok száma egész, ezért ebből az is következik, hogy ez a szám legfeljebb [3n/2].

1. ábra

Megmutatjuk, hogy ez az érték el is érhető. Ehhez először minden n≥3 egészhez konstruálunk egy n-szöget és hozzá egy e egyenest úgy, hogy e a sokszög minden oldalát metszi ha n páros, ha pedig n páratlan, akkor n-1 oldalt metsz. Ilyen sokszögek láthatók az 1. (n páratlan), illetve a 2. ábrán (n páros), a konstrukció az ábrák alapján nyilvánvaló. Ez a sokszög lesz a gúla alapsokszöge. Ezután felvesszük a gúla C csúcsát, majd pedig tekintünk egy olyan S síkot, amely az alapsokszög síkját e-ben metszi, C pedig azon az oldalán van, amelyiken az alapsokszögnek a nem több, azaz [n/2] csúcsa helyezkedik el. Ekkor S a gúlának n=2m esetén 2m alapélét és m oldalélét, azaz összesen 2m+m=3n/2 élét, n=2m+1 esetén pedig 2m alapélét és m+1 oldalélét, azaz összesen 2m+(m+1)=3n/2-1/2 élét metszi. Ez az érték mindkét esetben megegyezik [3n/2]-s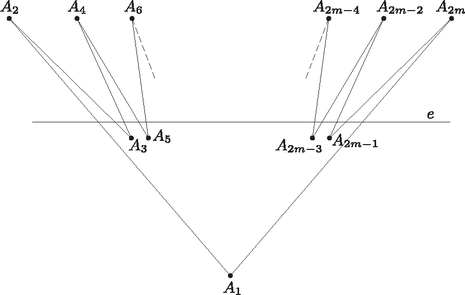zel.

2. ábra

 
Megjegyzés. Ha a gúla alaplapja konvex n-szög, akkor bármely sík a gúlának legfeljebb n+1 élét metszi. Ez pontosan úgy látható be, ahogy a B. 4294. feladat megoldásában (lásd 2011. áprilisi számunk 221. oldalán) megmutattuk, hogy egy 12 lapú konvex testnek egy sík legfeljebb 12 élét metszi. A két feladat egymás utáni hónapokban volt kitűzve, a gúlás feladatot a hasábos folytatásának tekintettük. Ezért azok a megoldók, akik csak konvex alapsokszög esetén oldották meg a feladatot, 0 pontot kaptak.