Feladat: B.4299 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bősze Zsuzsanna ,  Böőr Katalin ,  Damásdi Gábor ,  Énekes Péter ,  Kabos Eszter ,  Kiss Robin ,  Lajos Mátyás ,  Medek Ákos ,  Nagy Balázs ,  Nagy Róbert ,  Tossenberger Tamás ,  Varnyú József ,  Viharos Andor 
Füzet: 2011/május, 282 - 283. oldal  PDF  |  MathML 
Témakör(ök): Feladat, Beírt alakzatok, Középpontos és egyéb hasonlósági transzformációk, Síkgeometriai szerkesztések, Hossz, kerület
Hivatkozás(ok):Feladatok: 2010/október: B.4299

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

 
Megoldás. Legyen az AB oldal felezőpontja G, a C pont G-re vonatkozó tükörképe C', H pedig jelölje azt a pontot, melyre az FDAH négyszög paralelogramma. Először megmutatjuk, hogy H rajta van a CC' szakaszon.

 

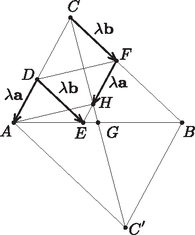1. ábra
 

Mivel DE párhuzamos CB-vel, az ADE és ACB háromszögek hasonlóak. Legyen a hasonlóság aránya λ. Ekkor 0<λ<1. Ha CA→=a és CB→=b, akkor tehát DA→=λa és DE→=λb. Ezért CD→=CA→-DA→=(1-λ)a, s így felhasználva, hogy a CDEF és az AHFD paralelogrammák szemközti oldalvektorai egyenlőek, kapjuk, hogy

CH→=CA→+AH→=a+DF→=a+CF→-CD→==a+DE→-CD→=a+λb-(1-λ)a=λ(a+b)=λCC'→.
Vagyis a H pont rajta van a CC' szakaszon.
Ezek alapján a szerkesztés menete a következő. Az A csúcs, mint középpont körül DF sugárral kört rajzolunk, a kör és a CC' szakasz H metszéspontján át AC-vel párhuzamos e egyenest szerkesztünk. Az e és AB, illetve CB metszéspontjai adják a szerkesztendő paralelogramma E, illetve F csúcsát. Végül az E-n át CB-vel húzott párhuzamos kimetszi CA-ból a D pontot.
 
Az így szerkesztett CDEF négyszög nyilván paralelogramma, s ha CH→=λCC'→=λ(a+b),
 
akkor a párhuzamosságok miatt DE→=CF→=λb és ezért DA→=λa. Ekkor viszont
DF→=λb-(1-λ)a=λ(a+b)-a=CH→-CA→=AH→,
vagyis DF ugyanolyan hosszú, mint AH, tehát a CDEF négyszög eleget tesz a feltételeknek.
A megoldások száma 2, 1 vagy 0, attól függően, hogy az A középpontú DF sugarú körnek és a nyílt CC' szakasznak hány közös pontja van. Ezt részletesebben az A-ból a CC' egyenesre bocsátott merőleges T talppontjának elhelyezkedését vizsgálva írhatjuk le.

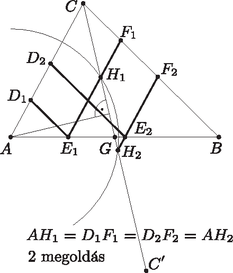2. ábra

 


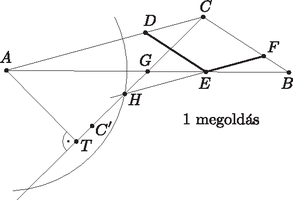3. ábra

•2 megoldás van, ha T a CC' szakasz belső pontja és AT<EF<min{AB,AC} (2. ábra).
•1 megoldás van, ha
∘T a CC' szakasz belső pontja és AT=EF;
∘T a CC' szakasz belső pontja és
AT<min{AB,AC}<EF<max{AB,AC};
∘T nem belső pontja a CC' szakasznak és AT≤min{AB,AC}<EF<max{AB,AC} (3. ábra).

•Ha az előző feltételek egyike sem teljesül, akkor nincs megoldás.

A DF átló hossza nyilván akkor minimális, ha AH minimális. Ismét megkülönböztetünk két esetet. Ha T a CC' szakasz belső pontja, akkor ez H≡T esetén következik be, ha pedig T nem belső pont, akkor az átló hosszának nincs minimuma. Ekkor DF legrövidebb hossza tetszőlegesen közel lehet az AB és AC oldalak közül a rövidebbikhez akkor, ha H tetszőlegesen közel van a C vagy a C' ponthoz, de minden esetben hosszabb lesz a két oldal közül a rövidebbiknél.